题目内容
10.计算:(1)$\frac{\sqrt{12}+\sqrt{18}}{\sqrt{3}}$-$\sqrt{\frac{1}{2}}$×$\sqrt{3}$
(2)已知x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,求x2+y2-xy-3x-3y的值.
分析 (1)根据混合运算的法则,先算乘除,再算加减;
(2)根据已知求得x-y=2$\sqrt{2}$,xy=1,然后原式变形为(x-y)2-3(x-y)+xy,代入即可求得.
解答 解:(1)原式=2+$\sqrt{6}$-$\frac{1}{2}$$\sqrt{6}$
=2+$\frac{\sqrt{6}}{2}$;
(2)∵x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,
∴x-y=$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$+$\sqrt{2}$=2$\sqrt{2}$,xy=($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=1,
原式=(x-y)2-3(x-y)+xy
=(2$\sqrt{2}$)2-3×2$\sqrt{2}$+1
=9-6$\sqrt{2}$.
点评 本题考查了二次根式的化简以及二次根式的混合运算,熟练掌握乘法公式和运算顺序是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.下列命题中,是真命题的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 相等的两个角是对顶角 | |
| D. | 从直线外一点到这条直线的垂线段,叫做这点到直线的距离 |
1.己知a2+3a-l=0,则a-$\frac{1}{a}$+2的值为( )
| A. | $\sqrt{5}$ | B. | -5 | C. | 1 | D. | -1 |
18.下列多项式中能用平方差公式因式分解的是( )
| A. | a2+(-b)2 | B. | 5m2-20mn | C. | -x2+9 | D. | -x2-y2 |
5.下列各点不在反比例函数y=-$\frac{1}{x}$的图象上的是( )
| A. | (-1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-$\frac{1}{2}$,2) |
19. 如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
 如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )
如图所示的旋转对称图形旋转一定角度后与自身重合,则这个角度至少是( )| A. | 30° | B. | 60° | C. | 120° | D. | 240° |
20.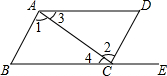 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )
①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
 如图,给出下列条件:其中,能判断AB∥DC的是( )
如图,给出下列条件:其中,能判断AB∥DC的是( )①∠1=∠2
②∠3=∠4
③∠B=∠DCE
④∠B=∠D.
| A. | ①或④ | B. | ②或③ | C. | ①或③ | D. | ②或④ |
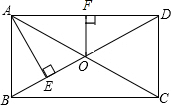 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.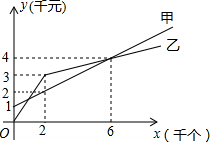 某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费
某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费