题目内容
3.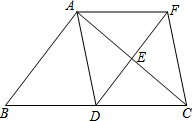 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
分析 (1)首先利用平行四边形的判定方法得出四边形ABDF是平行四边形,进而得出AF=DC,利用一组对边相等且平行的四边形是平行四边形,进而得出答案;
(2)利用等腰直角三角形的性质结合正方形的判定方法得出即可.
解答  (1)证明:∵点D、E分别是边BC、AC的中点,
(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)当△ABC是等腰直角三角形时,四边形ADCF是正方形,
理由:∵点D是边BC的中点,△ABC是等腰直角三角形,
∴AD=DC,且AD⊥DC,
∴平行四边形ADCF是菱形.
点评 此题主要考查了平行四边形的判定与性质以及正方形的判定,熟练应用平行四边形的判定与性质是解题关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
11.甲、乙两名运动员在某项射击比赛中10次射击的平均成绩都是7环,而甲、乙的成绩的方差分别为1.21和3.12,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
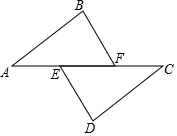 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.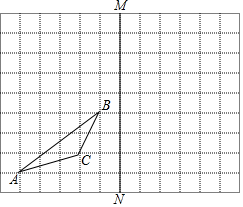 如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.
如图,已知三角形ABC和直线MN,且三角形ABC的顶点在网格的交点上.