题目内容
19.先阅读下列材料,然后回答后面问题:将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法.能分组分解的多项式通常有四项或六项,一般的分组分解有四种形式,即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等.
如“2+2”分法:
ax+ay+bx+by
=(ax+ay)+(bx+by)
=a(x+y)+b(x+y)
=(x+y)(a+b)
如“3+1”分法:
2xy+y2-1+x2
=x2+2xy+y2-1
=(x+y)2-1
=(x+y+1)(x+y-1)
请你仿照以上方法,探索并解决下列问题:
(1)分解因式:x2-y2-x-y;
(2)分解因式:45am2-20ax2+20axy-5ay2;
(3)分解因式:4a2+4a-4a2b-b-4ab+1.
分析 (1)首先利用平方差公式因式分解因式,进而提取公因式得出即可;
(2)将后三项运用完全平方公式分解因式进而利用平方差公式分解因式即可;
(3)重新分组利用完全平方公式分解因式得出即可.
解答 解:(1)x2-y2-x-y
=(x+y)(x-y)-(x+y)
=(x+y)(x-y-1);
(2)45am2-20ax2+20axy-5ay2
=45am2-5a(4x2-4xy+y2)
=5a[9m2-(2x-y)2]
=5a(3m-2x+y)(3m+2x-y);
(3)4a2+4a-4a2b-b-4ab+1
=(4a2+4a+1)-b(4a2+4a+1)
=(2a+1)2(1-b).
点评 此题主要考查了提取公因式法分解因式以及分组分解法分解因式,正确分组得出是解题关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
7.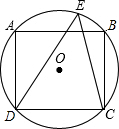 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
 如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )
如图,⊙O是正方ABCD的外接圆,点E是弧AB上任意一点,则∠DEC的度数为( )| A. | 40° | B. | 45° | C. | 48° | D. | 50° |
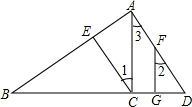 如图,已知:AB⊥AD,AC⊥BD,FG⊥BD,∠1=∠2,求证:CE⊥AB.
如图,已知:AB⊥AD,AC⊥BD,FG⊥BD,∠1=∠2,求证:CE⊥AB.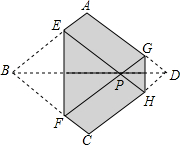 如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.
如图,菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点P处,折痕分别为EF、GH.重合点P在对角线BD上移动,设折痕EF的长为m.请你分别判断以下结论的真假,并给出理由.