题目内容
18.已知△ABC中,∠A=60°,角平分线BE、CF交于点O,则∠BOC=120°.分析 根据三角形内角和定理得到∠BOC=180°-(∠1+∠2),再根据角平分线得∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB),所以∠BOC=90°+$\frac{1}{2}$∠A,然后把∠A代入计算即可.
解答 解:∵角平分线BE、CF交于点O,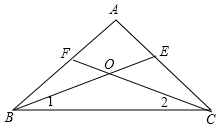
∴∠BOC=180°-(∠1+∠2)
=180°-$\frac{1}{2}$(∠ABC+∠ACB)
=180°-$\frac{1}{2}$(180°-∠A)
=180°-90°+$\frac{1}{2}$∠A
=90°+$\frac{1}{2}$×60°
=120°.
故答案为120°
点评 本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.下列计算结果是a8的值是( )
| A. | a2•a4 | B. | a2+a6 | C. | (a2)4 | D. | a9-a |
13.四边形分别具备下列条件,不能判断四边形是平行四边形的是( )
| A. | 两组对边分别相等 | B. | 两组对角相等 | ||
| C. | 两条对角线互相平分 | D. | 一组对边平行,另一组对边相等 |
3.若$\sqrt{a+b+5}$与|2a-b+1|互为相反数,则(b-a)2017的值为( )
| A. | -1 | B. | 1 | C. | 52015 | D. | -52015 |
10.关于x的方程2x-m=1的解是x=3,则m的值为( )
| A. | 5 | B. | -5 | C. | 7 | D. | -7 |
7.下列条件中,能判定四边形是平行四边形的是( )
| A. | 对角线互相平分 | B. | 对角线互相垂直 | ||
| C. | 对角线相等 | D. | 对角线互相垂直且相等 |
6.在数-3,2,-4中任取两个数相乘,其中积最小的是( )
| A. | -6 | B. | -12 | C. | -8 | D. | 12 |
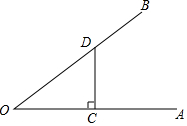 如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.
如图,OA、OB是两条射线,点C、D分别在OA、OB上,CD⊥OA,垂足为点C,OC=4,OD=5,若⊙P与OA、OB、CD都相切,则⊙P的半径是1或2.