题目内容
8.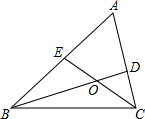 已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由.
已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由.
分析 在CB上取点G使得CG=CD,可证△BOE≌△BOG,得BE═BG,可证△CDO≌△CGO,得CD=CG,可以求得BE+CD=BC.
解答 解:在BC上取点G使得CG=CD,
∵∠BOC=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-60°)=120°,
∴∠BOE=∠COD=60°,
∵在△COD和△COG中,
$\left\{\begin{array}{l}{CO=CO}\\{∠DCO=∠GCO}\\{CD=CG}\end{array}\right.$,
∴△CODF≌△COG(SAS),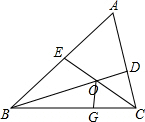
∴∠COG=∠COD=60°,
∴∠BOG=120°-60°=60°=∠BOE,
∵在△BOE和△BOG中,
$\left\{\begin{array}{l}{∠BOG=∠BOE}\\{BO=BO}\\{∠EBO=∠GBO}\end{array}\right.$,
∴△BOE≌△BOG(ASA),
∴BE=BG,
∴BE+CD=BG+CG=BC.
点评 本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质,本题中求证CD=CG和BE=BG是解题的关键.

练习册系列答案
相关题目
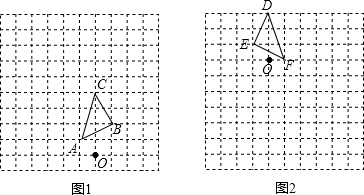
16.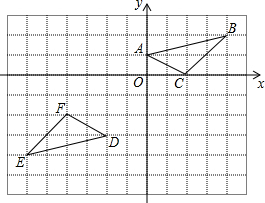 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )| A. | (-1,0) | B. | (-1,-1) | C. | (-2,-1) | D. | (-2,0) |

 已知正方形ABCD的边长为6,E、F分别为AD、CD的中点,AF、BE交于P,求CP的长.
已知正方形ABCD的边长为6,E、F分别为AD、CD的中点,AF、BE交于P,求CP的长.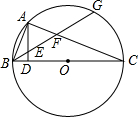 如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.
如图,BC是⊙O的直径,G为弧$\widehat{AC}$的中点,AD⊥BC于D,求证:AE=AF.