题目内容
11.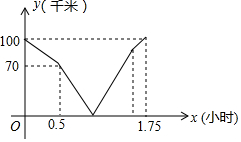 在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )| A. | 乙先出发的时间为0.5小时 | B. | 甲的速度是80千米/小时 | ||
| C. | 甲出发0.5小时后两车相遇 | D. | 甲到B地比乙到A地早$\frac{1}{12}$小时 |
分析 根据已知图象分别分析甲、乙两车的速度,进而分析得出答案.
解答 解:A、由图象横坐标可得,乙先出发的时间为0.5小时,正确,不合题意;
B、∵乙先出发,0.5小时,两车相距(100-70)km,∴乙车的速度为:60km/h,
故乙行驶全程所用时间为:$\frac{100}{60}$=1$\frac{2}{3}$(小时),
由最后时间为1.75小时,可得乙先到到达A地,
故甲车整个过程所用时间为:1.75-0.5=1.25(小时),
故甲车的速度为:$\frac{100}{1.25}$=80(km/h),
故B选项正确,不合题意;
C、由以上所求可得,甲出发0.5小时后行驶距离为:40km,乙车行驶的距离为:60km,40+60=100,故两车相遇,故C选项正确,不合题意;
D、由以上所求可得,乙到A地比甲到B地早:1.75-1$\frac{2}{3}$=$\frac{1}{12}$(小时),故此选项错误,符合题意.
故选:D.
点评 本题考查了利用函数的图象解决实际问题,解决本题的关键正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.

练习册系列答案
相关题目
1.我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
3.红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:

如图所示的扇形统计图中,扇形A对应的圆心角为72度,扇形B对应的圆心角为36度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
| 182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
| 175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
| 188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
| 谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
| 频数 | 3 | 8 | 10 | 6 | 3 |
| 对应扇形 图中区域 | B | D | E | A | C |

如图所示的扇形统计图中,扇形A对应的圆心角为72度,扇形B对应的圆心角为36度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
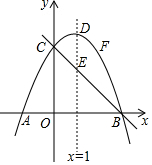 如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.
如图,抛物线y=ax2+bx+4(a≠0)与y轴交于C点,与x轴交于A(-2,0)、B两点,抛物线的对称轴直线x=1交抛物线于D点,交直线BC于E点.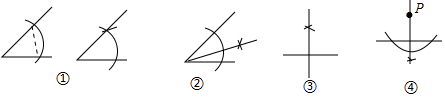
 小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.
小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为0.3km.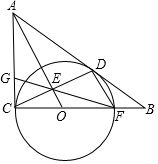 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.