题目内容
2.小明和小亮用如图所示的两个转盘做配紫色游戏,游戏规则是:分别转动两个转盘,若其中一个转盘转出红色,另一个转出蓝色,则可以配成紫色,此时小明得一分,否则小亮得一分.(1)用树状图或列表求出小明获胜的概率;
(2)这游戏对双方公平吗?请说明理由.若不公平,如何修改规则才能使游戏对双方公平?
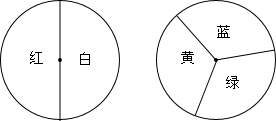
分析 (1)先利用列表法展示所有6种等可能的结果数,再找出可以配成紫色的结果数,然后根据概率公式计算小明获胜的概率;
(2)由于小明获胜的概率和小亮获胜的概率不相等,则可判断游戏不公平,可改为配成紫色小明得5分,否则小亮得1分.
解答 解:(1)列表如下:
| 黄 | 蓝 | 绿 | |
| 红 | (红,黄) | (红,蓝) | (红,绿) |
| 白 | (白,黄) | (白,蓝) | (白,绿) |
(2)不公平.因为P(配成紫色)≠P(没配成紫色).
修改:配成紫色小明得5分,否则小亮得1分.
点评 本题考查了游戏的公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了列表法与树状图法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列运算正确的是( )
| A. | 2(2x-3)=4x-3 | B. | 2x+3x=5x2 | C. | (x+1)2=x2+1 | D. | $\frac{1}{a-b}$+$\frac{1}{b-a}$=0 |
11.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
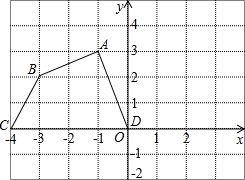 如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0)
如图,在平面直角坐标系中,四边形ABCD各个顶点的坐标分别为A(-1,3),B(-3,2),C(-4,0),D(0,0) 如图,矩形ABCD中,AD=5,AB=12,点E为CD上一个动点,把△ADE沿AE折叠,点D的对应点是D′,则CD′的最小值是8.
如图,矩形ABCD中,AD=5,AB=12,点E为CD上一个动点,把△ADE沿AE折叠,点D的对应点是D′,则CD′的最小值是8.