题目内容
18．化简$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷（m-1-$\frac{m-1}{m+1}$）的结果是$\frac{1}{m}$．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果．
解答 解：原式=$\frac{（m-1）^{2}}{（m+1）（m-1）}$÷$\frac{（m+1）（m-1）-m+1}{m+1}$=$\frac{m-1}{m+1}$•$\frac{m+1}{m（m-1）}$=$\frac{1}{m}$，
故答案为：$\frac{1}{m}$
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
过正方体中有公共顶点的三条棱的中点，切去一个三棱锥，形成如图的几何体，其展开图正确的是（ ）
9．如图是一组有规律的图案，第1个图案由4个▲组成，第2个图案由7个▲组成，第3个图案由10个▲组成，第4个图案由13个▲组成，…，则第n（n为正整数）个图案由（ ）个▲组成．
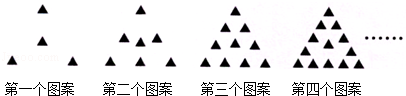
| A． | 4n+1 | B． | 3n+1 | C． | 4n-1 | D． | 3n-1 |
尺规作图：画出线段AB的垂直平分线（不写作法，保留作图痕迹）
13．tan45°的值等于（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{3}$ | C． | 1 | D． | $\sqrt{3}$ |
3．
如图是某射击选手5次射击成绩的折线图，根据图示信息，这5次成绩的众数、中位数分别是（ ）
如图是某射击选手5次射击成绩的折线图，根据图示信息，这5次成绩的众数、中位数分别是（ ）| A． | 7、9 | B． | 7、8 | C． | 8、9 | D． | 8、10 |
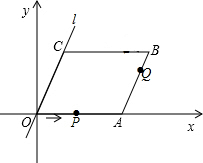如图，在平面直角坐标系中，四边形OABC是平行四边形，直线l经过O、C两点．点A的坐标为（8，0），点B的坐标为（11，4），动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动，同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动，过点P作PM垂直于x轴，与折线O一C-B相交于点M．当M、Q两点相遇时停止运动，设点P、Q运动的时间为t秒（t＞0）．△MPQ的面积为S．
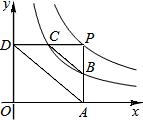如图，点P是反比例函数y=$\frac{6}{x}$（x＞0）的图象上任意一点，PA⊥x轴于A，PD⊥y轴于点D，分别交反比例函数y=$\frac{k}{x}$（x＞0，0＜k＜6）的图象于点B，C．下列结论：