题目内容
14.在同一平面内,两条直线相交时最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…,那么十条直线最多有( )| A. | 24个交点 | B. | 36个交点 | C. | 45个交点 | D. | 55个交点 |
分析 在同一平面内,直线相交时得到最多交点的方法是:每增加一条直线这条直线都要与之前的所有线段相交,即第n条直线时交点最多有1+2+3+4+…+(n-1)个,整理即可得到一般规律:$\frac{n(n-1)}{2}$,再把特殊值n=10代入即可求解.
解答 解:在同一平面内,两条直线相交时最多有1个交点,三条直线最多有3=1+2个交点,四条直线最多有6=1+2+3个交点,…,n条直线最多有1+2+3+4+…+(n-1)个交点,即1+2+3+4+…+(n-1)=$\frac{n(n-1)}{2}$.
当n=10时,$\frac{10(10-1)}{2}$=$\frac{90}{2}$=45
故选:C.
点评 本题主要考查直线的交点问题.注意直线相交时得到最多交点的方法是:每增加一条直线,这条直线都要与之前的所有线段相交.

练习册系列答案
相关题目
2.已知点P(a+1,2-a)到y轴的距离为2,则点P的坐标是( )
| A. | (-2,5) | B. | (1,1) | C. | (2,1) | D. | (-2,5)或(2,1) |
9.若关于x的分式方程$\frac{x}{x-5}$=3+$\frac{a}{5-x}$无解,则a的值为( )
| A. | a=5 | B. | a=-5 | C. | a=$\frac{1}{5}$ | D. | a=-$\frac{1}{5}$ |
19.按下面的程序计算:

如果输入x的值是正整数,输出结果是150,那么满足条件的x的值有( )

如果输入x的值是正整数,输出结果是150,那么满足条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列等式中,不是整式的是( )
| A. | $x-\frac{1}{2}y$ | B. | $\frac{3}{7}x$ | C. | $\frac{1}{x-1}$ | D. | 0 |
3.2015年10月8日,中国科学家屠呦呦获2015年诺贝尔生理学或医学奖,成为第一个获得诺贝尔自然学奖的中国人,获得奖金约300万元人民币,用科学记数法表示300万元为( )元.
| A. | 3×105 | B. | 3×106 | C. | 3×104 | D. | 30×105 |
 在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).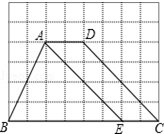 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.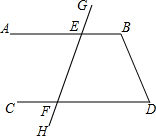 请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.
请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.