题目内容
2.已知点P(a+1,2-a)到y轴的距离为2,则点P的坐标是( )| A. | (-2,5) | B. | (1,1) | C. | (2,1) | D. | (-2,5)或(2,1) |
分析 根据点到y轴的距离是横坐标的绝对值,可得a的值,可得点的坐标.
解答 解:由点P(a+1,2-a)到y轴的距离为2,得
a+1=2或a+1=-2.
解得a=1,或a=-3.
点P的坐标是(2,1)或(-2,5),
故选:D.
点评 本题考查了点的坐标,利用点到y轴的距离是横坐标的绝对值得出a的值是解题关键.

练习册系列答案
相关题目
13.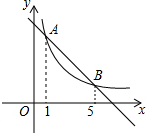 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
17.下列运算正确的是( )
| A. | (x+1)(x+1)=x2+1 | B. | (x-1)(x-1)=x2-1 | C. | (x+1)(x-1)=x2-1 | D. | (x+1)(x-1)=x2+1 |
7.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
| A. | (2,3) | B. | (-2,-3) | C. | (-3,2) | D. | (-3,-2) |
14.在同一平面内,两条直线相交时最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…,那么十条直线最多有( )
| A. | 24个交点 | B. | 36个交点 | C. | 45个交点 | D. | 55个交点 |
11.一个正多边形的每个外角都是72°,这个正多边形的边数是( )
| A. | 9 | B. | 10 | C. | 6 | D. | 5 |