题目内容
4. 在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).
在平面直角坐标系xOy中,定义直线y=ax+b为抛物线y=ax2+bx的特征直线,C(a,b)为其特征点.设抛物线y=ax2+bx与其特征直线交于A、B两点(点A在点B的左侧).(1)当点A的坐标为(0,0),点B的坐标为(1,3)时,特征点C的坐标为(3,0);
(2)若抛物线y=ax2+bx如图所示,请在所给图中标出点A、点B的位置;
(3)设抛物线y=ax2+bx的对称轴与x轴交于点D,其特征直线交y轴于点E,点F的坐标为(1,0),DE∥CF.
①若特征点C为直线y=-4x上一点,求点D及点C的坐标;
②若$\frac{1}{2}$<tan∠ODE<2,则b的取值范围是$-\frac{1}{2}≤b<0$或$\frac{5}{8}<b<4$.
分析 (1)根据点A、B求出直线解析式,得到a、b值,即可写出点C坐标;
(2)联立直线与抛物线解析式,即可求出点A(1,a+b),B(-$\frac{b}{a}$,0),根据图象描出两点即可;
(3)求出点D坐标,根据点F、C、E坐标及平行四边形性质,即可求出特征点C的坐标,根据已知和已证得:C(a,b),E(0,b),F(1,0),D(-$\frac{b}{2a}$,0),由CEDF平行四边形性质可以得出b关于a的函数关系式,利用已知$\frac{1}{2}$<tan∠ODE<2求出a的取值范围,进而求出b的取值范围;
解答 解:(1)∵A(0,0),B(1.3),
代入:直线y=ax+b,
解得:a=3,b=0,
∴直线y=3x,抛物线解析式:y=3x2,
∴C(3,0).
故答案为:(3,0);
(2)联立直线y=ax+b与抛物线y=ax2+bx,
得:ax2+(b-a)x-b=0,
∴(ax+b)(x-1)=0,
解得:x=-$\frac{b}{a}$,x=1,
∴A(1,a+b),B(-$\frac{b}{a}$,0).
点A、点B的位置如图所示;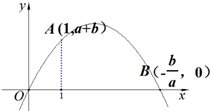
(3)①如图,
∵特征点C为直线y=-4x上一点,
∴b=-4a.
∵抛物线y=ax2+bx的对称轴与x轴交于点D,
∴对称轴$x=-\frac{b}{2a}=2$.
∴点D的坐标为(2,0).
∵点F的坐标为(1,0),
∴DF=1.
∵特征直线y=ax+b交y轴于点E,
∴点E的坐标为(0,b).
∵点C的坐标为(a,b),
∴CE∥DF.
∵DE∥CF,
∴四边形DECF为平行四边形.
∴CE=DF=1.
∴a=-1.
∴特征点C的坐标为(-1,4).
②由已知和已证得:
C(a,b),E(0,b),F(1,0),D(-$\frac{b}{2a}$,0),
∵$\frac{1}{2}$<tan∠ODE<2,
∴$\frac{1}{2}$<$\frac{OE}{OD}$<2,
∴$\frac{1}{2}$<|$\frac{b}{-\frac{b}{2a}}$|<2,
解得:$\frac{1}{2}$<|2a|<2,
∴-1<a<-$\frac{1}{4}$或$\frac{1}{4}$<a<1,
∵DE∥CF,CE∥DF,
∴CE=DF,
由题意可得:1+$\frac{b}{2a}$=a,(可以画出三种图象,由此得出这个结论)
整理得:b=2a2-2a
即:b=2(a-$\frac{1}{2}$)2-$\frac{1}{2}$
当b=2(a-$\frac{1}{2}$)2-$\frac{1}{2}$时,
当-1<a<-$\frac{1}{4}$,可得$\frac{5}{8}<b<4$.
当$\frac{1}{4}$<a<1时,可得-$\frac{1}{2}$≤b<0
综上所述:$\frac{5}{8}<b<4$或-$\frac{1}{2}$≤b<0.
点评 题目考查了新定义特征点、特征线及二次函数综合应用,题目整体难易适中,对学生最大的难点在于对新定义的理解.适合学生对中考压轴题目训练.

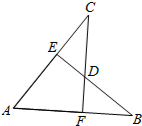 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论错误的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
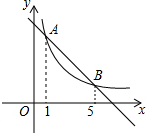 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,其横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}$+b的解集是( )| A. | -5<x<-1或x>0 | B. | 0<x<1或x>5 | C. | 1<x<5 | D. | -5<x<-1 |
| A. | 24个交点 | B. | 36个交点 | C. | 45个交点 | D. | 55个交点 |
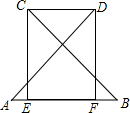 如图,已知:∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为E,F,AD=BC.求证:AE=BF.
如图,已知:∠A=∠B,CE⊥AB,DF⊥AB,垂足分别为E,F,AD=BC.求证:AE=BF.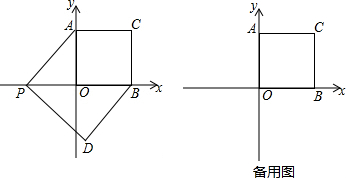

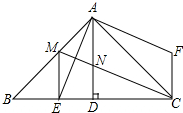 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.