题目内容
4.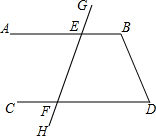 请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.
请补全证明过程.如图,已知线段AB,CD与GH相交于点E,F,∠GEB=?,∠EFD=β,∠D=50°,求∠B的度数.证明:∵∠GEB=β,∠EFD=β(已知)
∴∠GEB=∠EFD (等量代换)
∴AB∥CD (同位角相等,两直线平行)
∴∠D+∠B=180° (两直线平行,同旁内角互补)
又∵∠D=50° (已知)
∴∠B=180°-(50°)=(130°)(等式的性质)
分析 欲求∠B的度数,只需求得∠D的度数即可.
解答 证明:∵∠GEB=β,∠EFD=β(已知),
∴∠GEB=∠EFD(等量代换),
∴AB∥CD(同位角相等,两直线平行),
∴∠D+∠B=180°(两直线平行,同旁内角互补).
又∵∠D=50°(已知),
∴∠B=180°-(∠D或50°)=130°(等式的性质).
故答案是:等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;∠D或50°;130°;等式的性质.
点评 本题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
14.在同一平面内,两条直线相交时最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,…,那么十条直线最多有( )
| A. | 24个交点 | B. | 36个交点 | C. | 45个交点 | D. | 55个交点 |
16.直角三角形一边长为4,斜边长5,则面积为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.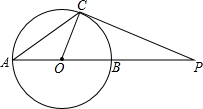 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
 如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )
如图,P是⊙O直径AB延长线上的一点,PC与⊙O相切于点C,若∠P=20°,则∠A的度数为( )| A. | 40° | B. | 35° | C. | 30° | D. | 25° |