题目内容
20.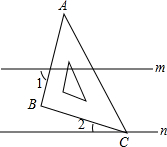 如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 延长AB交直线n于D,根据两直线平行,内错角相等可得∠3=∠1,再根据三角形的内角和等于180°列式计算即可得解.
解答  解:如图,延长AB交直线n于D,
解:如图,延长AB交直线n于D,
∵m∥n,
∴∠3=∠1,
∵△ABC是直角三角形,
∴∠ABC=90°,
∴∠2+∠3=180°-90°=90°,
∴∠1+∠2=90°.
故选D.
点评 本题考查了平行线的性质,三角形的内角和定理,熟记性质并作出辅助线构造出直角三角形是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
11.下列运算之前的倒数( )
| A. | x4-x3=x | B. | x2x3=x6 | C. | x5÷x3=x2 | D. | (x2)3=x5 |
15.已知抛物线C:y=x2+3x-10,将抛物线C平移得到抛物线C′,若两条抛物线C和C′关于直线x=1对称,则下列平移方法中,正确的是( )
| A. | 将抛物线C向右平移$\frac{5}{2}$个单位 | B. | 将抛物线C向右平移3个单位 | ||
| C. | 将抛物线C向右平移5个单位 | D. | 将抛物线C向右平移6个单位 |
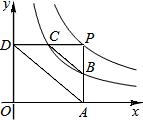 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论:
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上任意一点,PA⊥x轴于A,PD⊥y轴于点D,分别交反比例函数y=$\frac{k}{x}$(x>0,0<k<6)的图象于点B,C.下列结论: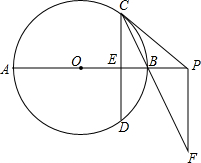 如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.
如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.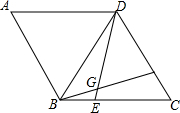 在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.
在菱形ABCD中,AB=BD,点E,F分别在BC,CD上,且BE=CF,连接BF,DE交于点G.若BG=3,DG=4,则四边形ABGD的面积为$\frac{49}{4}\sqrt{3}$.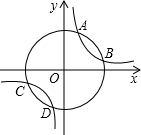 如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
如图,以原点为圆心的圆与反比例函数y=$\frac{3}{x}$的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )