题目内容

2．如图，PA和PB是⊙O的切线，点A和B是切点，AC是⊙O的直径，已知∠P=40°，则∠ACB的大小是（　　）
A．60°B．65°C．70°D．75°

分析 由PA、PB是⊙O的切线，可得∠OAP=∠OBP=90°，根据四边形内角和，求出∠AOB，再根据圆周角定理即可求∠ACB的度数．

解答 解：连接OB，
∵PA、PB是⊙O的切线，A、B为切点，
∴∠OAP=∠OBP=90°，
∴∠AOB=180°-∠P=140°，
由圆周角定理知，∠ACB=$\frac{1}{2}$∠AOB=70°，
故选C．

点评 本题考查了切线的性质，圆周角定理，解决本题的关键是连接OB，求出∠AOB，再根据圆周角定理来解答．

练习册系列答案
相关题目
13．七（2）数学测验成绩如下：77，74，65，53，95，87，84，63，91，53，69，81，61，69，91，78，75，81，80，67，76，81，61，69，79，94，86，70，70，87，81，86，90，88，85，67，71，82，87，75，落在79.5～89.5内数据的频数为14．
13．下列实数中，属于无理数的是（　　）
A．-$\frac{1}{3}$B．0.1C．$\sqrt{4}$D．$\root{3}{9}$
10．给出下列命题，其中，真命题的个数是（　　）
①平行四边形的对角线互相平分
②对角线相等的四边形是矩形
③菱形的对角线互相垂直平分
④对角线互相垂直且相等的四边形是正方形．
A．4个B．3个C．2个D．1个
17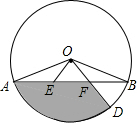．如图，AB是⊙O的弦，OA=10，F是线段AB上的点，且FB=FO，OF的延长线交⊙O于点D，∠B=30°，则阴影部分的面积为（　　）
A．25π-$\frac{100\sqrt{3}}{3}$B．25π-$\frac{50\sqrt{3}}{3}$C．30π-$\frac{25\sqrt{3}}{2}$D．20π-$\frac{50\sqrt{3}}{3}$
7．在平面直角坐标系中，点A、B的坐标分别为（a，0），（0，b），其中a，b满足$\sqrt{a-2b-18}$+|2a-5b-30|=0．将点B向右平移26个单位长度得到点C，如图①所示．
（1）求点A，B，C的坐标；
（2）点M，N分别为线段BC，OA上的两个动点，点M从点C向左以1.5个单位长度/秒运动，同时点N从点O向点A以2个单位长度/秒运动，如图②所示，设运动时间为t秒（0＜t＜15）．
①当CM＜AN时，求t的取值范围；
②是否存在一段时间，使得S四边形MNOB＞2S四边形MNAC？若存在，求出t的取值范围；若不存在，说明理由．
14．已知抛物线y=x2-（5+a）x+5a与x轴交于定点A和另一点C，
（1）求定点A的坐标；
（2）点B（1，2）是抛物线y=x2-（5+a）x+5a与以坐标原点为圆心的圆的一个交点，试判断直线AB与圆位置关系；
（3）在（2）中的抛物线上是否存在点P（P在点A的右上方），使△PAC、△PBC的面积相等？若存在，请求出点P的坐标，若不存在，请说明理由．
11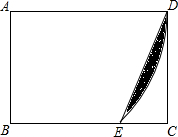．在矩形ABCD中，AB=$\sqrt{2}$，BC=2，以A为圆心，AD为半径画弧交线段BC于E，连接DE，则阴影部分的面积为（　　）
A．$\frac{π}{2}$-$\sqrt{2}$B．$\frac{π}{2}$-$\frac{\sqrt{2}}{2}$C．π-$\sqrt{2}$D．π-$\frac{\sqrt{2}}{2}$
12．若不等式组$\left\{\begin{array}{l}2x-4≤0\\ 1+x＞a\end{array}\right.$有解，则a的取值范围是（　　）
A．a≤3B．a＜3C．a＜2D．a≤2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网