题目内容
20.$\frac{x-1}{{x}^{2}+x-6}$,$\frac{2}{{x}^{2}-9}$,$\frac{x-2}{{x}^{2}+5x+6}$的最简公分母是( )| A. | (x+3)2(x+2)(x-2) | B. | (x2-9)2(x2-4) | C. | (x2-9)2(x-4)2 | D. | (x+3)2(x-3)2(x2+2)(x-2) |
分析 要求分式的最简公分母,即取各分母系数的最小公倍数与字母因式的最高次幂的积.
解答 解:∵$\frac{x-1}{{x}^{2}+x-6}$=$\frac{x-1}{(x+3)(x-2)}$,
$\frac{2}{{x}^{2}-9}$=$\frac{2}{(x+3)(x-3)}$,
$\frac{x-2}{{x}^{2}+5x+6}$=$\frac{x-2}{(x+3)(x+2)}$,
∴$\frac{x-1}{{x}^{2}+x-6}$,$\frac{2}{{x}^{2}-9}$,$\frac{x-2}{{x}^{2}+5x+6}$的最简公分母是(x2-9)2(x2-4);
故选B.
点评 此题考查了最简公分母,①如果各分母都是单项式,那么最简公分母就是各系数的最小公倍数,相同字母的最高次幂,所有不同字母都写在积里.②如果各分母都是多项式,就可以将各个分母因式分解,取各分母数字系数的最小公倍数,凡出现的字母(或含字母的整式)为底数的幂的因式都要取最高次幂.

练习册系列答案
相关题目
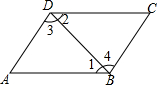 已知:如图,AB∥CD,AB=CD.求证:AD∥BC.
已知:如图,AB∥CD,AB=CD.求证:AD∥BC.