题目内容
2.$-\frac{1}{3}$的绝对值是$\frac{1}{3}$;-(-$1\frac{2}{3}$)的相反数是$-1\frac{2}{3}$.分析 利用绝对值和相反数的定义解答即可.
解答 解:$-\frac{1}{3}$的绝对值是$\frac{1}{3}$;
∵-(-$1\frac{2}{3}$)=1$\frac{2}{3}$,
∴-(-$1\frac{2}{3}$)的相反数是-1$\frac{2}{3}$,
故答案为:$\frac{1}{3}$;$-1\frac{2}{3}$.
点评 本题主要考查了绝对值和相反数的定义,理解定义是解答此题的关键.

练习册系列答案
相关题目
20.$\frac{x-1}{{x}^{2}+x-6}$,$\frac{2}{{x}^{2}-9}$,$\frac{x-2}{{x}^{2}+5x+6}$的最简公分母是( )
| A. | (x+3)2(x+2)(x-2) | B. | (x2-9)2(x2-4) | C. | (x2-9)2(x-4)2 | D. | (x+3)2(x-3)2(x2+2)(x-2) |
7.要使△ABC≌△A′B′C′,需要满足的条件是( )
| A. | AB=A′B′,∠B=∠B′,AC=A′C′ | B. | AB=A′B′,∠A=∠A′,BC=B′C′ | ||
| C. | AC=A′C′,∠C=∠C′,BC=B′C′ | D. | AC=A′C′,∠B=∠B′,BC=B′C′ |
12.若有理数m<n,在数轴上点M表示数m,点N表示数n,则M与N的位置关系为( )
| A. | 点M在点N的右边 | B. | 点M在点N的左边 | ||
| C. | 点M在原点右边,点N在原点左边 | D. | 点M和点N都在原点右边 |
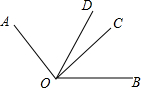 如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.
如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数. 如图,在△ABC中,P为AB上的一点,在下列条件中:
如图,在△ABC中,P为AB上的一点,在下列条件中: