Question

10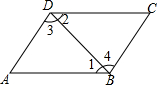．已知：如图，AB∥CD，AB=CD．求证：AD∥BC．
证明：∵AB∥CD
∴∠ABD=∠BDC（两直线平行，内错角相等）
在△ABD和△CDB中，
（AB）=（CD），
（∠ABD）=（∠BDC），
（BD）=（BD），
∴△ABD≌△△CDB（SAS）
∴∠ADB=∠CBD（全等三角形对应角相等）
∴AD∥BC（内错角相等，两直线平行）．

Answer 1

分析 根据两直线平行，内错角相等求出∠ABD=∠BDC，再证明△ABD和△CDB全等，然后根据全等三角形对应角相等得出∠ADB=∠CBD，进一步得出AD∥BC．

解答 证明：∵AB∥CD
∴∠ABD=∠BDC（两直线平行，内错角相等），
在△ABD和△CDB中，
$\left\{\begin{array}{l}{AB=CD}\\{∠ABD=∠BDC}\\{BD=BD}\end{array}\right.$，
∴△ABD≌△CDB（SAS），
∴∠ADB=∠CBD（全等三角形对应角相等），
∴AD∥BC（内错角相等，两直线平行）．
故答案为：ABD；BDC；两直线平行，内错角相等；AB；CD；∠ADB；∠BDC；BD；BD，SAS；ADB；CBD；全等三角形对应角相等；内错角相等，两直线平行

点评 本题主要考查了三角形全等的判定和性质；平行线的性质与判定，找准内错角是解决问题的关键．