题目内容
18.已知一个直角三角形的两边长分别为3和4,则这个三角形斜边上的高为$\frac{3\sqrt{7}}{4}$或$\frac{12}{5}$.分析 分为两种情况:①斜边是4有一条直角边是3,再由三角形面积即可得出结果;②3和4都是直角边,根据勾股定理求出斜边,由勾股定理即可得出结果.
解答 解:分为两种情况:
①斜边是4有一条直角边是3,
由勾股定理得:第三边长=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴斜边上的高为$\frac{3×\sqrt{7}}{4}$=$\frac{3\sqrt{7}}{4}$;
②3和4都是直角边,
由勾股定理得:第三边长=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴斜边上的高为$\frac{3×4}{5}$=$\frac{12}{5}$;
故答案为:$\frac{3\sqrt{7}}{4}$或$\frac{12}{5}$.
点评 本题考查的是勾股定理以及三角形面积的计算方法;熟练掌握勾股定理是解决问题的关键,注意分类讨论.

练习册系列答案
相关题目
8.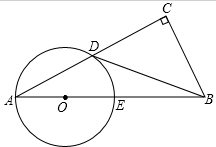 如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(I)求证:BD与⊙O相切.
(2)若点D是AC的中点.求tan∠DBA的值.
 如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
如图,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,过点A,D作⊙O,使圆心O在AB上,⊙O与AB交于点E.(I)求证:BD与⊙O相切.
(2)若点D是AC的中点.求tan∠DBA的值.
13.关于x的一元二次方程x2-5x+p2-2p+5=0的一个根为1,则实数p的值是( )
| A. | 4 | B. | 1 | C. | 0或2 | D. | -1 |
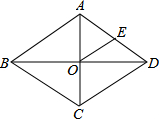 如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5.
如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于3.5. 如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数.
如图所示,AB与CD相交于点O,OE平分∠AOD,若∠BOD=40°,求∠AOC,∠AOE的度数. 如图,在?ABCD中,对角线AC,BD相交于点O,△AOB的周长是10cm,AB=3cm,AD=5cm,试求△AOD的周长.
如图,在?ABCD中,对角线AC,BD相交于点O,△AOB的周长是10cm,AB=3cm,AD=5cm,试求△AOD的周长.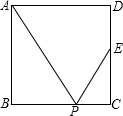 如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( )
如图所示,四边形ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件:①∠APB=∠EPC;②∠APE=∠APB;③P是BC的中点;④BP:BC=2:3,其中能推出△ABP∽△ECP的有( ) 如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.
如图所示,矩形ABCD的对角线AC,BD的交点O,点E、F、G、H分别是AO、BO、OC、OD的中点.