题目内容
16.不等式组$\left\{\begin{array}{l}{3x-2(2x-1)<3}\\{\frac{x+1}{2}≤1}\end{array}\right.$的解集是-1<x≤1.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{3x-2(2x-1)<3①}\\{\frac{x+1}{2}≤1②}\end{array}\right.$,
∵解不等式①得:x>-1,
解不等式②得:x≤1,
∴不等式组的解集为-1<x≤1,
故答案为:-1<x≤1.
点评 本题考查了解一元一次不等式(组)的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
6.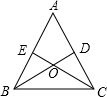 如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是( )
如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是( )
 如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是( )
如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②③ |
5.在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
| A. | 1 | B. | 1或$\frac{\sqrt{3}-1}{2}$ | C. | 1或$\frac{\sqrt{3}+1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$或$\frac{\sqrt{3}+1}{2}$ |
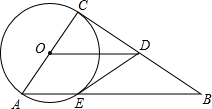 如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:
如图,Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证: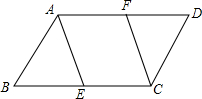 如图,在?ABCD中,点E、F分别是BC、AD的中点
如图,在?ABCD中,点E、F分别是BC、AD的中点