题目内容
10．在Rt△ABC中，∠C=90°，AB=2BC，现给出下列结论：①sinA=$\frac{1}{2}$；②cosB=$\frac{\sqrt{3}}{2}$；③tanA=$\frac{\sqrt{3}}{3}$；④tanB=$\sqrt{3}$，其中正确的结论是（ ）| A． | ①②③ | B． | ①②④ | C． | ②③④ | D． | ①③④ |
分析 直接利用直角三角形的性质结合特殊角的三角函数值得出答案．
解答 
解：∵在Rt△ABC中，∠C=90°，AB=2BC，
∴∠A=30°，
∴①sinA=$\frac{BC}{AB}$=$\frac{1}{2}$，正确；②cosB=$\frac{BC}{AB}$=$\frac{1}{2}$，故此选项错误；
③tanA=tan30°=$\frac{\sqrt{3}}{3}$，正确；④tanB=tan60°=$\sqrt{3}$，正确．
故选：D．
点评 此题主要考查了直角三角形的性质和特殊角的三角函数值，正确记忆相关数据是解题关键．
练习册系列答案
相关题目
20．
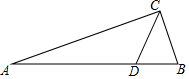如图所示，在Rt△ABC中，斜边AB=3，BC=1，点D在AB上，且$\frac{BD}{AD}$=$\frac{1}{3}$，则tan∠BCD的值是（ ）
如图所示，在Rt△ABC中，斜边AB=3，BC=1，点D在AB上，且$\frac{BD}{AD}$=$\frac{1}{3}$，则tan∠BCD的值是（ ）| A． | $\frac{1}{3}$ | B． | 1 | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{3\sqrt{3}}{2}$ |
如图，直线AB与CD相交于点O，射线OE平分∠BOD，若∠DOE=20°，则∠AOC=40°，∠BOC=140°．
15．下列以a，b，c为三边的三角形中，是直角三角形的是（ ）
| A． | $a=\sqrt{3}$，$b=\sqrt{4}$，$c=\sqrt{5}$ | B． | a=1，b=2，$c=2\sqrt{5}$ | C． | a=2，b=3，$c=\sqrt{5}$ | D． | a=1，$b=2\sqrt{2}$，c=2 |