题目内容
19.两个相似三角形的相似比等于1:4,则其对应的周长比为1:4.分析 根据相似三角形周长的比等于相似比进行解答即可.
解答 解:∵两个相似三角形的相似比为1:4,
∴它们对应周长的比为1:4.
故答案为:1:4.
点评 本题考查的是相似三角形的性质,即相似三角形周长的比等于相似比.

练习册系列答案
相关题目
10.在Rt△ABC中,∠C=90°,AB=2BC,现给出下列结论:①sinA=$\frac{1}{2}$;②cosB=$\frac{\sqrt{3}}{2}$;③tanA=$\frac{\sqrt{3}}{3}$;④tanB=$\sqrt{3}$,其中正确的结论是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
8.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{8}$ |
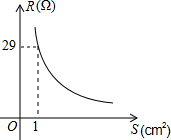 实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为,当S=2cm2时,R=14.5Ω.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为,当S=2cm2时,R=14.5Ω. 如图:△ABC中,点D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=60°,∠1=52°,则∠2=112°.
如图:△ABC中,点D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A=60°,∠1=52°,则∠2=112°. 看图并按要求解决问题:
看图并按要求解决问题: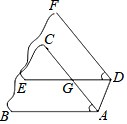 如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.
如图,某同学剪了两片角度均为50°的硬板纸纸片(∠BAC=∠EDF=50°),将其中一片平移,连结AD,如果△AGD中有两个角相等,则∠GAD的度数为50°或80°或65°.