题目内容
20.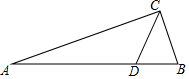 如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )
如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
分析 作DE∥AC,根据平行线分线段成比例定理求得BE=$\frac{1}{4}$,CE=$\frac{3}{4}$,BD=$\frac{3}{4}$,然后根据勾股定理求得DE,根据正切函数等于对边比邻边,可得答案.
解答  解:作DE∥AC,
解:作DE∥AC,
∵在Rt△ABC中,斜边AB=3,BC=1,
∴DE∥AC,
∴$\frac{BE}{CE}$=$\frac{BD}{AD}$=$\frac{1}{3}$,
∴BE=$\frac{1}{4}$,CE=$\frac{3}{4}$,BD=$\frac{3}{4}$
∴DE=$\sqrt{B{D}^{2}-B{E}^{2}}$=$\frac{\sqrt{2}}{2}$,
∴tan∠BCD=$\frac{DE}{CE}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{3}{4}}$=$\frac{2\sqrt{2}}{3}$.
故选C.
点评 本题考查了解直角三角形,锐角三角函数的定义是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

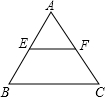 如图所示,刘伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是25 米.
如图所示,刘伯伯家有一块等边三角形的空地ABC,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是25 米. 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )
如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )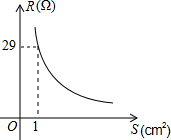 实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为,当S=2cm2时,R=14.5Ω.
实验表明,当导线的长度一定时,导线的电阻与它的横截面积成反比例.一条长为100cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示,那么,其函数关系式为,当S=2cm2时,R=14.5Ω.