题目内容
3.一组数据4,5,3,4,4的中位数、众数和方差分别是( )| A. | 3,4,0.4 | B. | 4,0.4,4 | C. | 4,4,0.4 | D. | 4,3,0.4 |
分析 根据中位数、众数和方差的概念求解.排序后的第3个数是中位数;出现次数最多的数据是众数;方差公式为:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].
解答 解:把这组数据从小到大排列:3,4,4,4,5,最中间的数是4,则这组数据的中位数是4;
4出现了2次,出现的次数最多,则众数是4;
平均数是(4+5+3+4+4)÷5=4,所以方差为S2=$\frac{1}{5}$[[(4-4)2+(5-4)2+(3-4)2+(4-4)2+(4-4)2]=0.4.
故选C.
点评 此题考查了中位数、众数和方差,将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;众数是一组数据中出现次数最多的数;方差公式为:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

练习册系列答案
相关题目
15.下列各数中最小的数是( )
| A. | -π | B. | -3 | C. | -$\sqrt{5}$ | D. | 0 |
12.计算(x2)3÷(-x)2的结果是( )
| A. | x2 | B. | x3 | C. | -x3 | D. | x4 |
 如图,△ABC中,CE和CF分别平分∠ACB和△ABC的外角∠ACD,一动点O在AC上运动,过点O作BD的平行线与∠ACB和∠ACD的角平分线分别交于点E和点F.
如图,△ABC中,CE和CF分别平分∠ACB和△ABC的外角∠ACD,一动点O在AC上运动,过点O作BD的平行线与∠ACB和∠ACD的角平分线分别交于点E和点F.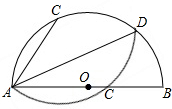 如图,半圆O的直径AB=10cm,D为$\widehat{AB}$上一点,C为$\widehat{AD}$上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为4$\sqrt{5}$cm.
如图,半圆O的直径AB=10cm,D为$\widehat{AB}$上一点,C为$\widehat{AD}$上一点,把弓形沿直线AD翻折,C和直径AB上的点C′重合,若AC=6cm,则AD的长为4$\sqrt{5}$cm. 如图,菱形ABCD的对角线交于点O,AC=16cm,BD=12cm.
如图,菱形ABCD的对角线交于点O,AC=16cm,BD=12cm.