Question

11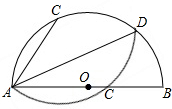．如图，半圆O的直径AB=10cm，D为$\widehat{AB}$上一点，C为$\widehat{AD}$上一点，把弓形沿直线AD翻折，C和直径AB上的点C′重合，若AC=6cm，则AD的长为4$\sqrt{5}$cm．

Answer 1

分析 连接OD，OC，作DE⊥AB于E，OF⊥AC于F，运用圆周角定理，可证得∠DOB=∠OAC，即证△AOF≌△OED，所以OE=AF=3cm，根据勾股定理，得DE=4cm，在直角三角形ADE中，根据勾股定理，可求AD的长．

解答 解：连接OD，OC，作DE⊥AB于E，OF⊥AC于F，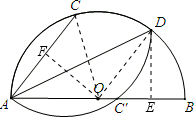

∵∠CAD=∠BAD（折叠的性质），
∴$\widehat{CD}$=$\widehat{BD}$，
∴点D是$\widehat{BC}$的中点．
∴∠DOB=∠OAC=2∠BAD，
∴△AOF≌△OED，
∴OE=AF=$\frac{1}{2}$AC=$\frac{1}{2}$AC'=3cm，
在Rt△DOE中，DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=4cm，
在Rt△ADE中，AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=4$\sqrt{5}$cm．
故答案是：4$\sqrt{5}$cm．

点评 本题考查了翻折变换及圆的有关计算，涉及圆的题目作弦的弦心距是常见的辅助线之一，注意熟练运用垂径定理、圆周角定理和勾股定理．