题目内容
18.计算(1)22+(-9)×($\frac{1}{3}$)
(2)$\frac{1}{2}$x3y2•4x2y2
(3)tm+1•t+(-t)2•tm(m为整数)
(4)(a+b+c)2-(a+b-c)2
(5)(2a-3b)(3a+2b)
(6)(2a-b-3)(2a+b-3)
(7)(x-3)(x2-9)(3+x)
分析 (1)先算乘方和乘法,再算加法;
(2)利用同底数幂的乘法计算;
(3)先利用同底数幂的乘法计算,再进一步合并即可;
(4)利用完全平方公式计算,再进一步合并;
(5)利用整式的乘法计算方法计算即可;
(6)(7)利用平方差公式计算即可.
解答 解:(1)原式=4-3
=1;
(2)原式=2x5y4;
(3)原式=tm+2+tm+2
=2tm+2;
(4)原式=(a+b)2+2c(a+b)+c2-(a+b)2+2c(a+b)-c2
=4c(a+b)
=4ac+4bc;
(5)原式=6a2-5ab-6b2;
(6)原式=(2a-3)-b
=4a2-12a-b2+9;
(7)原式=(x2-9)(x2-9)
=x4-18x2+81.
点评 此题考查整式的混合运算,掌握运算顺序,正确判定运算符号,利用计算方法和计算公式计算即可.

练习册系列答案
相关题目
6.不论x取何值,下列分式中一定有意义的是( )
| A. | $\frac{x-1}{x^2}$ | B. | $\frac{x+1}{x-1}$ | C. | $\frac{x+1}{|x|-1}$ | D. | $\frac{x-1}{|x|+1}$ |
13.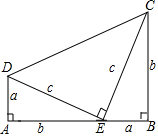 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
 用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )
用两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图,通过用不同的方法计算这个图形的面积,可以得到哪一个等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)(a+b)=a2-b2 | C. | a2+b2=c2 | D. | c2-a2=(c-a)(c+a) |
3.计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(101)2表示二进制数,将它转换成十进制形式是:1×22+0×21+1×20=5,那么将二进制数(1101)2转换成十进制数是( )
| A. | 13 | B. | 12 | C. | 11 | D. | 9 |
8.下列各式中正确的是( )
| A. | $\frac{x+y}{x+y}=0$ | B. | $\frac{y}{x}=\frac{{y}^{2}}{{x}^{2}}$ | C. | $\frac{-x+y}{-x-y}=1$ | D. | $\frac{1}{-x+y}=-\frac{1}{x-y}$ |
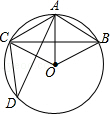 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论:
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论: