题目内容
15. 如图所示,AB、AC是⊙O的切线,B、C是切点,∠BAC=70°,点P是⊙O上不同于B、C的任意一点,求∠BPC的度数.
如图所示,AB、AC是⊙O的切线,B、C是切点,∠BAC=70°,点P是⊙O上不同于B、C的任意一点,求∠BPC的度数.
分析 连接OB、OC,如图,根据切线的性质得∠ABO=90°,∠ACO=90°,则根据四边形内角和得到∠AOB=180°-∠A=110°,然后分类讨论:当P在优弧BC上时,根据圆周角定理易得∠BPC=$\frac{1}{2}$∠BOC=55°,当P在劣弧BC上时,即P′点处,则利用圆内接四边形的性质易得∠BP′C=180°-∠BPC=125°.
解答 解:连接OB、OC,如图,
∵AB、AC是⊙O的切线,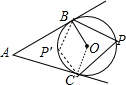
∴OB⊥AB,OC⊥AC,
∴∠ABO=90°,∠ACO=90°,
∴∠AOB=180°-∠A=180°-70°=110°,
当P在优弧BC上时,∠BPC=$\frac{1}{2}$∠BOC=55°,
当P在劣弧BC上时,即P′点处,∠BP′C=180°-∠BPC=125°,
综上所述,∠BPC的度数为55°或125°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆周角定理.注意分类讨论思想的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )


| A. | 2014 | B. | 2013 | C. | 2012 | D. | 2011 |
6.一个三角形三条边上的高之比为2:3:4,那么三条边之比是( )
| A. | 6:4:3 | B. | 1:2:3 | C. | 1:1:2 | D. | 2:2:3 |

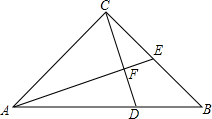 如图,点D是等腰Rt△ABC的斜边AB上的一点,AB=3BD,AF⊥CD于点F交BC于点E.
如图,点D是等腰Rt△ABC的斜边AB上的一点,AB=3BD,AF⊥CD于点F交BC于点E. 如图,在矩形ABCD中,E是边CD的中点.BF⊥AE.垂足为点F.设AB=a,BC=b,求BF的长.
如图,在矩形ABCD中,E是边CD的中点.BF⊥AE.垂足为点F.设AB=a,BC=b,求BF的长.