Question

20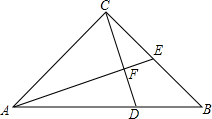．如图，点D是等腰Rt△ABC的斜边AB上的一点，AB=3BD，AF⊥CD于点F交BC于点E．
（1）求证：E是BC的中点；
（2）求AF：CF的值；
（3）求DF：CF的值．

Answer 1

分析 （1）作BP⊥BC交CD的延长线于P，如图1，先由AC∥BP得$\frac{BP}{AC}$=$\frac{AD}{BD}$，由于AB=3BD，则AD=2BD，AC=2BP，所以BC=2BP，再证明△ACE≌△CBP得到CE=BP，则BC=2CE，于是可判断
E是BC的中点；
（2）证明Rt△ACF∽△CEF，则$\frac{AF}{CF}$=$\frac{AC}{CE}$，而BC=AC=2CE，易得$\frac{AF}{CF}$=2；
（3）作DH∥AE交BC于H，如图2，根据平行线分线段成比例定理得$\frac{BH}{BE}$=$\frac{BD}{BA}$=$\frac{1}{3}$，则EH=$\frac{2}{3}$BE，再由EF∥DH，然后利用平行线分线段成比例定理即可得到$\frac{DF}{CF}$=$\frac{EH}{CE}$=$\frac{2}{3}$．

解答 （1）证明：作BP⊥BC交CD的延长线于P，如图1，
∵∠ACB=90°，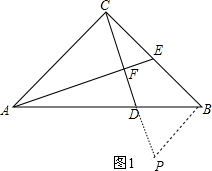
∴AC∥BP，
∴$\frac{BP}{AC}$=$\frac{AD}{BD}$，
∵AB=3BD，
∴AD=2BD，
∴AC=2BP，
而AC=BC，
∴BC=2BP，
∵AF⊥CD，
∴∠CAF+∠ACF=90°，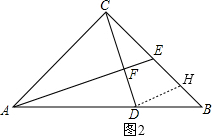
而∠ACF+∠ECF=90°，
∴∠CAF=∠ECF，
在△ACE和△CBP中，
$\left\{\begin{array}{l}{∠ACE=∠CBP}\\{AC=CB}\\{∠CAE=∠BCP}\end{array}\right.$，
∴△ACE≌△CBP，
∴CE=BP，
∴BC=2CE，
∴E是BC的中点；
（2）解：∵∠CAF=∠ECF，
∴Rt△ACF∽△CEF，
∴$\frac{AF}{CF}$=$\frac{AC}{CE}$，
而BC=AC=2CE，
∴$\frac{AF}{CF}$=2；
（3）解：作DH∥AE交BC于H，如图2，
∴$\frac{BH}{BE}$=$\frac{BD}{BA}$=$\frac{1}{3}$，
∴EH=$\frac{2}{3}$BE，
∵EF∥DH，
∴$\frac{DF}{CF}$=$\frac{EH}{CE}$=$\frac{\frac{2}{3}BE}{CE}$=$\frac{2}{3}$．

点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例．也考查了三角形全等的判定与性质．