题目内容
16．已知：A（0，1），B（1，0），C（3，2）．（1）求△ABC的面积；
（2）设点P在坐标轴上，且△ABP与△ABC的面积相等，直接写出点P的坐标．
分析 （1）根据图形的面积的和差计算即可．
（2）分点P在x轴上和点P在y轴上两种情况讨论可得符合条件的点P的坐标．
解答 
解：（1）S△ABC=2×3-$\frac{1}{2}×$1×3-$\frac{1}{2}$×2×2-$\frac{1}{2}×$1×1=2；
（2）∵点P在坐标轴上，△ABP与△ABC的面积相等，
∴P1（-3，0）、P2（5，0）、P3（0，5）、P4（0，-3）．
点评 本题考查了坐标与图形性质以及图形的面积的计算，不规则图形的面积等于规则图形的面积的和或差．
练习册系列答案
相关题目
4．把$\frac{{-\sqrt{45{y^2}}}}{{3\sqrt{5y}}}$化简后得（ ）
| A． | $\frac{{-\sqrt{9y}}}{3}$ | B． | $-\sqrt{y}$ | C． | $-3\sqrt{5y}$ | D． | $\frac{{3\sqrt{5}}}{5}$ |
8．若在数轴上画出表示下列各数的点，则与原点距离最近的点是（ ）
| A． | -1 | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 2 |
5．
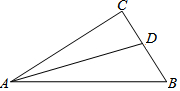如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）
如图，在Rt△ABC中，∠C=90°，AD是△ABC的角平分线，若CD=4，AC=12，AB=15，则△ABC的面积为（ ）| A． | 48 | B． | 50 | C． | 54 | D． | 60 |