��Ŀ����
10��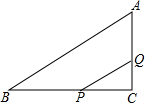 ��ͼ��ʾ���ڡ�ABC�У���C=90�㣬BC=8���ף�AC=6���ף���P��B���������ÿ��2�����ٶ���BC��C���ƶ�����Q��C���������ÿ��1�����ٶ���CA��A���ƶ���
��ͼ��ʾ���ڡ�ABC�У���C=90�㣬BC=8���ף�AC=6���ף���P��B���������ÿ��2�����ٶ���BC��C���ƶ�����Q��C���������ÿ��1�����ٶ���CA��A���ƶ�����1����AB�ij���
��2�������P��Q�ֱ��B��Cͬʱ���������˶���ʱ��Ϊx�룬��PCQ�����Ϊy�����y����x�ĺ�������ʽ����д��������
��3����xΪ��ֵʱ����PCQ����һ�����Ϊ30���ֱ�������Σ�
���� ��1�����ù��ɶ�����֪AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10cm��
��2������y=$\frac{1}{2}$•PC•CQ���㼴�ɣ������P���˶�ʱ�伴��֪���Ա���x��ȡֵ��Χ��
��3�����������ηֱ��г����̼��㼴�ɣ�
��� �⣻��1����Rt��ABC�У� �ߡ�C=90�㣬BC=8cm��AC=6cm��
�ߡ�C=90�㣬BC=8cm��AC=6cm��
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10cm��
��2����CQ=x��PB=2x��
��y=$\frac{1}{2}$•PC•CQ=$\frac{1}{2}$��8-2x��•x=-x2+4x��
���P�˶�����C��ʱ��Ϊ4s��
��0��x��4��
��3���ٵ���QPC=30��ʱ����֪PC=$\sqrt{3}$CQ����8-2x=$\sqrt{3}$x�����x=8��$\sqrt{3}$-2����
�ڵ���PQC=30��ʱ��CQ=$\sqrt{3}$PC����x=$\sqrt{3}$��8-2x�������x=$\frac{48-8\sqrt{3}}{11}$��
����������x=8��$\sqrt{3}$-2��s��$\frac{48-8\sqrt{3}}{11}$sʱ����PCQ����һ�����Ϊ30���ֱ�������Σ�
���� ���⿼���������ۺ��⡢���ɶ�����ֱ��������30�Ƚ����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п��������ͣ�

| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
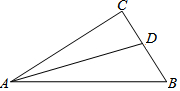 ��ͼ����Rt��ABC�У���C=90�㣬AD�ǡ�ABC�Ľ�ƽ���ߣ���CD=4��AC=12��AB=15�����ABC�����Ϊ��������
��ͼ����Rt��ABC�У���C=90�㣬AD�ǡ�ABC�Ľ�ƽ���ߣ���CD=4��AC=12��AB=15�����ABC�����Ϊ��������| A�� | 48 | B�� | 50 | C�� | 54 | D�� | 60 |
| A�� | a2��a3=a6 | B�� | $\sqrt{\frac{3}{2}}��\sqrt{2}=\frac{{\sqrt{3}}}{2}$ | C�� | $\frac{x-1}{{1-{x^2}}}=\frac{1}{x+1}$ | D�� | ��x+y��2=x2+y2 |
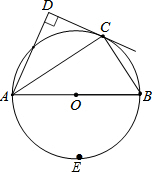 ��ͼ�����ı���ABCD�У���D=90�㣬ACƽ�֡�DAB���ҵ�C����ABΪֱ���ġ�O�ϣ�
��ͼ�����ı���ABCD�У���D=90�㣬ACƽ�֡�DAB���ҵ�C����ABΪֱ���ġ�O�ϣ�