Question

10．如图所示网格是由边长为1的小正方形组成，点A，B，C位置如图所示，在网格中确定点D，使以A，B，C，D为顶点的四边形的所有内角都相等．
（1）确定点D的位置并画出以A，B，C，D为顶点的四边形；
（2）直接写出（1）中所画出的四边形的周长和面积．

Answer 1

分析 （1）根据题意可知以A，B，C，D为顶点的四边形是矩形，作出矩形ABCD即为所求；
（2）根据勾股定理可求AB、CD的长度，再根据进行的周长公式和面积公式计算即可求解．

解答 解：（1）如图所示：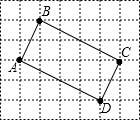

（2）AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，
BC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$，
周长为（2$\sqrt{5}$+$\sqrt{5}$）×2=6$\sqrt{5}$，
面积为2$\sqrt{5}$×$\sqrt{5}$=10．

点评 考查了勾股定理，本题关键是得到以A，B，C，D为顶点的四边形是矩形，以及由勾股定理求得AB、CD的长度．