题目内容
3.计算:(1)(-$\frac{1}{2}$)-1-(-$\frac{2}{3}$)2015×(1.5)2016+20160
(2)$\sqrt{48}-\sqrt{54}÷\sqrt{2}-|1-\sqrt{3}|$.
分析 (1)分别根据0指数幂及负整数指数幂的计算法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先去绝对值符号,再把各根式化为最减二次根式,由实数混合运算的法则进行计算即可.
解答 解:(1)原式=-2-[(-$\frac{2}{3}$)×1.5]2015×1.5+1
=-2+$\frac{3}{2}$+1
=$\frac{1}{2}$;
(2)原式=$\sqrt{48}$-$\sqrt{27}$-($\sqrt{3}$-1)
=$\sqrt{48}$-$\sqrt{27}$-$\sqrt{3}$+1
=4$\sqrt{3}$-3$\sqrt{3}$-$\sqrt{3}$+1
=1.
点评 本题考查的是实数的运算,熟知0指数幂及负整数指数幂的计算法则是解答此题的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
13.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | $(\frac{1}{x})^{2}+\frac{1}{x}-2=0$ | C. | 3(x+1)2=2(x+1) | D. | 2x2+3x=2x2-2 |
18.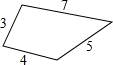 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
 如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )
如图,长度分别为3,4,5,7的四条线段首尾相接,相邻两线段的夹角可调整,则任意两端点的距离最大值为( )| A. | 7 | B. | 9 | C. | 10 | D. | 12 |
8. 如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
 如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )
如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )| A. | 0 | B. | 2$\sqrt{5}$ | C. | 4-2$\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
15.在-3x,6-a=2,4ab2,0,$\frac{m-3}{m}$,$\frac{1}{2}$,$\frac{1}{2}$>$\frac{1}{3}$,x中,是代数式的共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
13.某学校组织了一次知识竞赛,初二年级、初三年级各10名选手的比赛成绩如下(本次竞赛满分10分):
(1)初二成绩的中位数是9.5分,初三成绩的众数是10分;
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.
| 初二 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 初三 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)运用学过的数学知识说明、判断,哪个年级选手的成绩整体比较稳定.