题目内容
15.在-3x,6-a=2,4ab2,0,$\frac{m-3}{m}$,$\frac{1}{2}$,$\frac{1}{2}$>$\frac{1}{3}$,x中,是代数式的共有( )| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
分析 代数式:代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子.单独的一个数或者一个字母也是代数式.带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式.依此即可求解.
解答 解:在-3x,6-a=2,4ab2,0,$\frac{m-3}{m}$,$\frac{1}{2}$,$\frac{1}{2}$>$\frac{1}{3}$,x中,是代数式的有-3x,4ab2,0,$\frac{m-3}{m}$,$\frac{1}{2}$,x,共有6个.
故选:B.
点评 考查了代数式,注意:①不包括等于号(=)、不等号(≠、≤、≥、<、>、≮、≯)、约等号≈. ②可以有绝对值.例如:|x|,|-2.25|等.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.浙江省委作出“五水共治”决策.某广告公司用形状大小完全相同的材料分别制作了“治污水”、“防洪水”、“排涝水”、“保供水”、“抓节水”5块广告牌,从中随机抽取一块恰好是“治污水”广告牌的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
20. 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
 函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2-4c<0;
②b+c=0;
③2b+c<-2;
④当x>3时,x2+(b-1)x+c<0.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )
如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )
 如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )
如图,点A在第一象限,以点A为顶点的抛物线经过原点,与x轴的正半轴交于点B,对称轴为x=1,点C在抛物线上,且位于点A,O之间(点C与A,O不重合),若△AOC的周长为m,则四边形ACOB的周长为( )| A. | m | B. | m+1 | C. | m+2 | D. | m+3 |
5. 如图,在△ABC中,点D在BC上,∠DAC=∠B,BD=4,DC=5,DE∥AC交AB于点E,则DE的长为( )
如图,在△ABC中,点D在BC上,∠DAC=∠B,BD=4,DC=5,DE∥AC交AB于点E,则DE的长为( )
 如图,在△ABC中,点D在BC上,∠DAC=∠B,BD=4,DC=5,DE∥AC交AB于点E,则DE的长为( )
如图,在△ABC中,点D在BC上,∠DAC=∠B,BD=4,DC=5,DE∥AC交AB于点E,则DE的长为( )| A. | $\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 3 | D. | 4 |
 如图,AD是⊙O的直径,以AD为边作平行四边形ABCD,AB与⊙O交于点F,在边
如图,AD是⊙O的直径,以AD为边作平行四边形ABCD,AB与⊙O交于点F,在边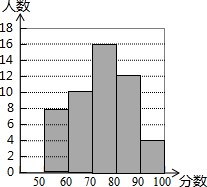 本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题:
本学期初,我市教育部门对某中学从学生的品德、身心、学习、创新、国际、审美、信息、生活八个方面进行了综合评价,评价小组从八年级学生中选取部分学生针对“信息素养”进行测试,并将测试结果绘制成如下统计图(如图).根据图中信息,解答下列问题: