题目内容
3.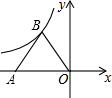 等边△OAB的边长为2,顶点A在x轴负半轴上,反比例函数y=$\frac{k}{x}$的图象经过顶点B,则k的值为y=-$\frac{\sqrt{3}}{x}$.
等边△OAB的边长为2,顶点A在x轴负半轴上,反比例函数y=$\frac{k}{x}$的图象经过顶点B,则k的值为y=-$\frac{\sqrt{3}}{x}$.
分析 过B作BM⊥AO于点M,根据等边三角形的性质和A点坐标求出B点坐标,然后用待定系数法求出解析式.
解答 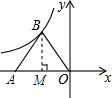 解:过B作BM⊥AO于点M,
解:过B作BM⊥AO于点M,
∵△OAB为等边三角形,
∴AB=BO=AO=2,
∵BM⊥OA,
∴OM=$\frac{1}{2}$OA=1,
∴BM=$\sqrt{{OB}^{2}-{OM}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
则点B的坐标为(-1,$\sqrt{3}$)
则这个反比例函数的解析式为y=-$\frac{\sqrt{3}}{x}$.
故答案为:y=-$\frac{\sqrt{3}}{x}$.
点评 此题考查的是反比例函数图象上点的坐标特点,涉及到等边三角形的性质,以及待定系数法求函数关系式,解决问题的关键是根据等边三角形的性质求出B点的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.若一个角的补角比这个角的余角的2倍多20°15′,则这个角的余角的度数是( )
| A. | 20°15′ | B. | 70°45′ | C. | 69°85′ | D. | 69°45′ |
18.在我校主办的校园达人秀总决赛中,14名参赛选手成绩统计情况如表,这14名选手成绩的中位数和众数是
( )
( )
| 分数 | 80 | 85 | 90 | 95 | 98 |
| 人数 | 2 | 4 | 5 | 2 | 1 |
| A. | 85,90 | B. | 90,90 | C. | 85,87.5 | D. | 87.5,90 |
15. 边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
 边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
12.不等式组$\left\{\begin{array}{l}{2(x-1)>x}\\{x≤\frac{x+3}{2}}\end{array}\right.$的解是$\frac{1}{2}$<x≤3.
13.若代数式2a2-a+3的值为5,则代数式4a2-2a+6的值为( )
| A. | -22 | B. | 10 | C. | -10 | D. | 22 |
 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点.已知B(24,0),C(0,10),则⊙A的半径为13.
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点.已知B(24,0),C(0,10),则⊙A的半径为13.