题目内容
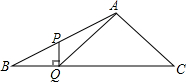 在△ABC中,∠B=30°,P为AB上的一点,
在△ABC中,∠B=30°,P为AB上的一点,| BP |
| AP |
| 1 |
| 2 |
考点:相似三角形的判定与性质,勾股定理,锐角三角函数的定义
专题:
分析:过A作AD⊥BC于点D,根据平行线分线段成比例可得到AD与PQ的关系,根据含特殊角的直角三角形的性质可得到PQ和AQ的关系,在Rt△ADQ中可求得答案.
解答: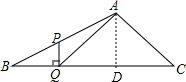 解:
解:
过A作AD⊥BC于点D,
∵PQ⊥BC,
∴AD∥PQ,
∴
=
=
,
=
=
=
,
∴QD=2BQ,AD=3PQ,
在Rt△PBQ中,∠B=30°,
∴BQ=
PQ,
∴QD=2
PQ,
在Rt△ADQ中,由勾股定理可得AQ=
PQ,
∴cos∠AQC=
=
=
.
 解:
解:过A作AD⊥BC于点D,
∵PQ⊥BC,
∴AD∥PQ,
∴
| BQ |
| QD |
| BP |
| AP |
| 1 |
| 2 |
| PQ |
| AD |
| BP |
| AB |
| BP |
| AP+PB |
| 1 |
| 3 |
∴QD=2BQ,AD=3PQ,
在Rt△PBQ中,∠B=30°,
∴BQ=
| 3 |
∴QD=2
| 3 |
在Rt△ADQ中,由勾股定理可得AQ=
| 21 |
∴cos∠AQC=
| QD |
| AQ |
2
| ||
|
2
| ||
| 7 |
点评:本题主要考查平行线分线段性质及三角函数的定义,掌握平行线分线段所得线段对应成比例是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
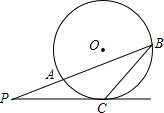 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
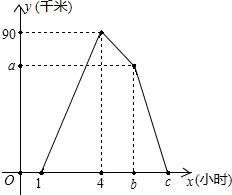 甲、乙两人同时从家乘车去县城,途中甲因故下车,改骑自行车前往县城(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达县城停留1小时后,以另一速度返回,1小时后与甲相遇.如图为甲、乙两人之间的距离y(千米)与行驶时间x(小时)之间的函数关系.
甲、乙两人同时从家乘车去县城,途中甲因故下车,改骑自行车前往县城(换车的时间不计).已知甲骑自行车的速度为15千米/小时,乙到达县城停留1小时后,以另一速度返回,1小时后与甲相遇.如图为甲、乙两人之间的距离y(千米)与行驶时间x(小时)之间的函数关系.