题目内容
二次函数y=-2x2-4x+1,当-3≤x≤0时,求它的最大值与最小值.
考点:二次函数的最值
专题:
分析:易求得二次函数的对称轴,根据对称轴在区间[-3,0]内,即可求得二次函数的最大值,再根据二次函数关于对称轴对称,找到距离对称轴最远的点即可求得当-3≤x≤0时,二次函数的最小值,即可解题.
解答:解:∵二次函数y=-2x2-4x+1对称轴为y=-
=-1,且a=-2<0,
∴当-3≤x≤0时,x=-1,二次函数有最大值为-2+4+1=3,
∵|-3-(-1)|=2,|0-(-1)|=1,
∴当-3≤x≤0时,x=-3时,二次函数有最小值为-18+12+1=-5,
综上所述,二次函数y=-2x2-4x+1,当-3≤x≤0时,它的最大值为3,最小值为-5.
| b |
| 2a |
∴当-3≤x≤0时,x=-1,二次函数有最大值为-2+4+1=3,
∵|-3-(-1)|=2,|0-(-1)|=1,
∴当-3≤x≤0时,x=-3时,二次函数有最小值为-18+12+1=-5,
综上所述,二次函数y=-2x2-4x+1,当-3≤x≤0时,它的最大值为3,最小值为-5.
点评:本题考查了二次函数对称轴的求解,考查了二次函数的最值问题,本题中求得二次函数的对称轴是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
抛物线y=2(x+3)2的顶点坐标是( )
| A、(3,0) |
| B、(0,3) |
| C、(-3,0) |
| D、(0,-3) |
下列计算正确的是( )
A、2
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
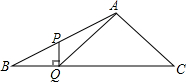 在△ABC中,∠B=30°,P为AB上的一点,
在△ABC中,∠B=30°,P为AB上的一点,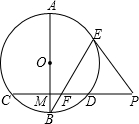 如图,AB是⊙O的直径,弦CD⊥AB于M,P是CD延长线上一点,PE切⊙O于E,BE交CD于F.求证:PF2=PD•PC.
如图,AB是⊙O的直径,弦CD⊥AB于M,P是CD延长线上一点,PE切⊙O于E,BE交CD于F.求证:PF2=PD•PC.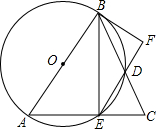 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,连接BE、ED,过点B的直线交ED的延长线于F,且∠DBF=∠BED.