题目内容
4. (1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长;
(1)已知:如图,点C在线段AB上,AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长;(2)根据第(1)题的计算过程和结果,设AC+BC=a,其他条件不变,你能求出MN的长吗?请用一句话表达你的发现;
(3)如果第(1)题的叙述改为:“已知点C在直线AB上,线段AC=6,BC=4,点M、N分别是AC、BC的中点,求MN的长.”结论会起变化吗?如果变化,求出MN的长.
分析 (1)根据点M、N分别是AC、BC的中点,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度即可;
(2)根据点M、N分别是AC、BC的中点,可知CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,再利用MN=CM+CN即可求出MN的长度;
(3)根据题意画出图形,求出CM及CN的长,再由MN=CM-CN即可得出结论.
解答 解:(1)∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC=3,
CN=$\frac{1}{2}$BC=2cm,
∴MN=CM+CN=3+2=5;
(2)猜测MN=$\frac{1}{2}$a,
∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC,
CN=$\frac{1}{2}$BC,
∴MN=CM+CN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$a;
(3)会起变化.
如图所示,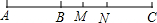
∵AC=6,BC=4,点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC=3,CN=$\frac{1}{2}$BC=2,
∴MN=CM-CN=3-2=1.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13.计算-5a5b3c÷(15a4b3)的结果是( )
| A. | 3ac | B. | -3ac | C. | $\frac{1}{3}$ac | D. | -$\frac{1}{3}$ac |
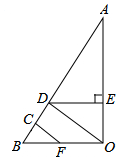 如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO,
如图,已知:DE⊥AO于点E,BO⊥AO于点O,∠CFB=∠EDO, 如图,A、B、C、D四点在一条直线上.
如图,A、B、C、D四点在一条直线上. 已知一辆装满货物的卡车高2.5米,宽1.6米,要开进某一如图所示的桥洞,问这辆卡车能否经过桥洞?说明理由.
已知一辆装满货物的卡车高2.5米,宽1.6米,要开进某一如图所示的桥洞,问这辆卡车能否经过桥洞?说明理由.