题目内容
10.已知:如图,正比例函数y1=kx(k>0)的图象与反比例函数y2=$\frac{6}{x}$的图象相交于点A和点C,设点C的坐标为(2,n).(1)①求k与n的值;②试利用函数图象,直接写出不等式kx-$\frac{6}{x}$<0的解集;
(2)点B是x轴上的一个动点,连结AB、BC,作点A关于直线BC的对称点Q,在点B的移动过程中,是否存在点B,使得四边形ABQC为菱形?若存在,求出点B的坐标;若不存在,请说明理由.
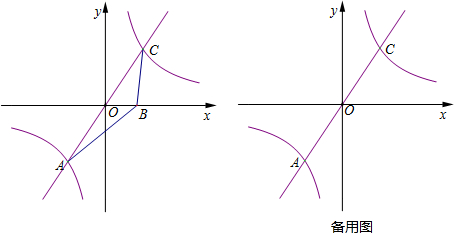
分析 (1)①由点C的坐标为(2,n),在反比例函数y2=$\frac{6}{x}$的图象上,可求得点C的坐标,又由点C在正比例函数y1=kx(k>0)的图象上,即可求得答案;
②直接利用图象,即可求得不等式kx-$\frac{6}{x}$<0的解集;
(2)分别从点B在x轴的正半轴与点B在x轴的负半轴,去分析求解即可求得答案.
解答 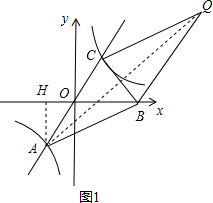 解:(1)①把点C的坐标为(2,n)代入${y_2}=\frac{6}{x}$,
解:(1)①把点C的坐标为(2,n)代入${y_2}=\frac{6}{x}$,
解得:n=3
∴点C的坐标为(2,3),
把点C(2,3)代入y1=kx得:3=2k,
解得:k=$\frac{3}{2}$;
②由两函数图象可知,kx-$\frac{6}{x}$<0的解集是:x<-2或0<x<2;
(2)如图1,当点B在x轴的正半轴且AB=AC时,四边形ABQC为菱形.
∵点A与点Q关于直线BC对称,
∴AC=QC,AB=QB,
∴AC=QC=AB=QB.
∴四边形ABQC为菱形.
由(1)中点C的坐标(2,3),
可求得:OC=$\sqrt{13}$,
∵点A与点C关于原点对称,
∴点A的坐标为(-2,-3),
∴OA=OC=$\sqrt{13}$,AC=2$\sqrt{13}$,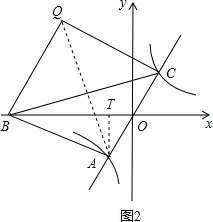
∴AC=AB=2$\sqrt{13}$.
作AH⊥x轴于点H,则AH=3.
在Rt△AHB中,由勾股定理得:BH=$\sqrt{({2\sqrt{13})}^{2}-{3}^{2}}$=$\sqrt{43}$,
又∵OH=2,
∴OB=BH-OH=$\sqrt{42}$-2,
∴点B的坐标为$({\sqrt{43}-2,\;0})$,
如图2,当点B在x轴的负半轴且AB=AC时,四边形ABQC为菱形.作AT⊥x轴于点T,
同理可求得:$BT=\sqrt{{{({2\sqrt{13}})}^2}-{3^2}}=\sqrt{43}$,
又∵OT=2,
∴$OB=BT+OT=\sqrt{43}+2$,
∴点B的坐标为$({-\sqrt{43}-2,\;0})$,
综上,当点B的坐标为$({\sqrt{43}-2,\;0})$或$({-\sqrt{43}-2,\;0})$时,四边形ABQC为菱形.
点评 此题属于反比例函数综合题.考查了待定系数求函数解析式、反比例函数与一次函数的交点问题以及菱形的性质.注意掌握分类讨论思想的应用是解此题的关键.

 考前必练系列答案
考前必练系列答案| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | 2 | D. | ±2 |
| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
 如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.
如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.
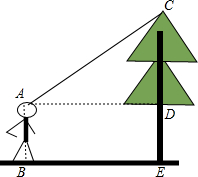 如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73)
如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73)