题目内容
20.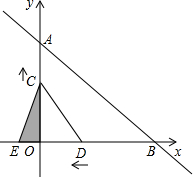 如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.
如图,已知直线y=kx+b与坐标轴分别交于点A(0,8)、B(8,0),动点 C从原点O出发沿OA方向以每秒1个单位长度向点A运动,动点D从点B出发沿BO方向以每秒1个单位长度向点O运动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动,设运动时间为t 秒.(1)直接写出直线的解析式:y=-x+8;
(2)若E点的坐标为(-2,0),当△OCE的面积为5 时.
①求t的值;
②探索:在y轴上是否存在点P,使△PCD的面积等于△CED的面积?若存在,请求出P点的坐标;若不存在,请说明理由.
分析 (1)由点A、B的坐标,利用待定系数法求出直线解析式即可;
(2)①根据运动的规律,找出点C的坐标,根据△OCE的面积为5利用三角形的面积公式即可得出关于t的一元一次方程,解方程即可得出结论;
②假设存在,设点P的坐标为(0,m),结合①结论找出点C、D的坐标,根据三角形面积相等结合三角形的面积公式即可得出关于m的含绝对值的一元一次方程,解方程即可得出结论.
解答 解:(1)将点A(0,8)、B(8,0)代入y=kx+b中,
得:$\left\{\begin{array}{l}{8=b}\\{0=8k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=8}\end{array}\right.$,
∴该直线的解析式为y=-x+8.
故答案为:y=-x+8.
(2)①由已知得:点C(0,t)(0≤t≤8),点E(-2,0),
∴OC=t,OE=2.
∵S△OCE=$\frac{1}{2}$OE•OC=$\frac{1}{2}$×2t=5,
∴t=5.
②假设存在,设点P的坐标为(0,m),如图所示.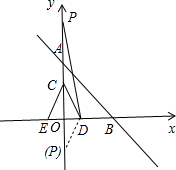
由①可知t=5,此时点C(0,5),点D(3,0),
∴OC=5,DE=5,OD=3.
S△DCE=$\frac{1}{2}$OC•DE=$\frac{1}{2}$×5×5=$\frac{25}{2}$,S△DCP=$\frac{1}{2}$OD•PC=$\frac{1}{2}$×3×|m-5|.
∵S△DCE=S△DCP,
∴$\frac{25}{2}$=$\frac{1}{2}$×3×|m-5|,即3|m-5|=25,
解得:m=-$\frac{10}{3}$或$\frac{40}{3}$.
故当△OCE的面积为5时,在y 轴存在点P,使△PCD的面积等于△CED的面积,点P的坐标为(0,-$\frac{10}{3}$)或(0,$\frac{40}{3}$).
点评 本题考查了待定系数法求函数解析式、三角形的面积公式以及解一元一次方程,解题的关键是:(1)利用待定系数法求出函数解析式;(2)①得出关于t的一元一次方程;②得出关于m的方程3|m-5|=25.本题属于中档题,难度不大,解决该题型题目时,根据三角形面积间的关系结合三角形的面积公式找出方程是关键.

 名校课堂系列答案
名校课堂系列答案| A. | (x-8)2=16 | B. | (x-8)2=20 | C. | (x-4)2=16 | D. | (x-4)2=20 |
| A. | a2+b2>2ab | B. | a2+b2≥2ab | C. | (a+b)2>2ab | D. | (a+b)2≥2ab |
| A. | 有无数对 | B. | 只有一对 | C. | 只有三对 | D. | 以上都不对 |
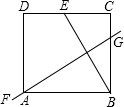 如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )
如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
 如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).
如图,边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2),B(1,3).