Question

18．已知：在△ABC中，
（1）AC=BC，∠ACB=90°，CD⊥AB，点E是AB边上一点，点F在线段CE上，且△CBF≌△EBF（如图①），求证：CE平分∠ACD；
（2）除去（1）中条件“AC=BC”，其余条件不变（如图②），上述结论是否成立？并说明理由．

Answer 1

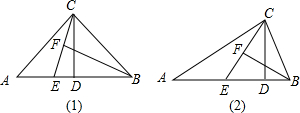
分析 （1）先证明△CBF≌△EBF，再根据外角的性质，得∠BEF=∠A+∠ACE，即可得出∠ACE=∠DCE，则CE平分∠ACD；
（2）假设结论依然成立，由△CBF≌△EBF，得∠BCF=∠BEF，再由外角，得∠BEF=∠A+∠ACE，即可得出CE平分∠ACD．

解答 （1）证明：∵AC=BC，∠ACB=90°，∠A=∠ABC=45°，
∵CD⊥AB，
∴∠CDB=90°，
∴∠BCD=45°，
∴∠BCD=∠A，
∵△CBF≌△EBF，
∴∠BCF=∠BEF
∵∠BEF是△ACE的外角，
∴∠BEF=∠A+∠ACE，
又∵∠BCF=∠BCD+∠DCE
∴∠A+∠ACE=∠BCD+∠DCE
∴∠ACE=∠DCE
∴CE平分∠ACD；
（2）上述结论依然成立，
∵∠ACB=90°，CD⊥AB，
∴∠A+∠ABC=90°，∠BCD+∠ABC=90°，
∴∠BCD=∠A．
∵△CBF≌△EBF，
∴∠BCF=∠BEF
∵∠BEF是△ACE的外角，
∴∠BEF=∠A+∠ACE，
又∵∠BCF=∠BCD+∠DCE
∴∠A+∠ACE=∠BCD+∠DCE
∴∠ACE=∠DCE
∴CE平分∠ACD．

点评 本题考查了全等三角形的判定和性质，以及角平分线的性质，掌握全等的判定方法是解题的关键．