题目内容
12.若x是不等于1的实数,我们把$\frac{1}{1-x}$称为x的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数为$\frac{1}{1-(-1)}$=$\frac{1}{2}$,现已知x1=-$\frac{1}{3}$,x2是x1的差倒数,x3是x2的差倒数,x4是x3的差倒数,…,依此类推,则x2015=$\frac{3}{4}$.分析 根据已知条件可以先计算出几个x的值,从而可以发现其中的规律,求出x2015的值.
解答 解:由已知可得,
x1=-$\frac{1}{3}$,
x2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
x3=$\frac{1}{1-\frac{3}{4}}$=4,
x4=$\frac{1}{1-4}$=-$\frac{1}{3}$,
可知每三个一个循环,
2015÷3=671…2,
故x2015=$\frac{3}{4}$.
点评 本题考查实数的性质,解题的关键是发现其中的规律,求出相应的x的值.

练习册系列答案
相关题目
11.从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3千米,平路每小时走4千米,下坡每小时走5千米,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟.根据以上条件,下列说法不正确的是( )
| A. | 设上坡路长x千米,可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$ | |
| B. | 设上坡路长x千米,平路长y千米,可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$ | |
| C. | 列算式(54-42)÷(5-3)即可求出上坡路长. | |
| D. | 根据条件,能求出甲地到乙地的全程是3.1千米. |
1. 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )
 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )| A. | ∠B=∠ACB | B. | ∠A=∠ACE | C. | ∠B=∠ACE | D. | ∠A=∠ECD |
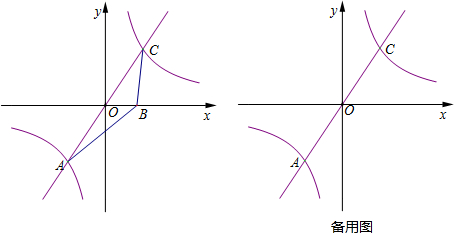
 如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(秒).
如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(秒). 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.