题目内容
如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么需要测量________才能测得A,B之间的距离( )
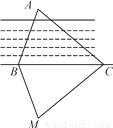
A. AB B. AC C. BM D. CM
 C
【解析】∵∠ABC=∠CBM=70°,BC=BC,∠ACB=∠MCB=40°,
∴△ABC≌△MBC,∴AB=BM,
所以需要测量BM的长才能测得A、B之间的距离,
故选C.
C
【解析】∵∠ABC=∠CBM=70°,BC=BC,∠ACB=∠MCB=40°,
∴△ABC≌△MBC,∴AB=BM,
所以需要测量BM的长才能测得A、B之间的距离,
故选C.
下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. 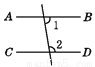 B.
B. 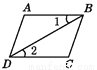 C.
C. 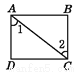 D.
D. 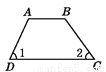
 B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B
B
【解析】试题分析:利用平行线的判定方法判断即可.
【解析】
如图所示:
∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
故选B 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
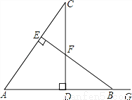
 (1)138°;(2)3.
【解析】试题分析:(1)根据全等求出∠EBA的度数,根据邻补角的定义求出即可;
(2)根据全等三角形的性质得出AC=AB=9,AE=AD=6,即可求出答案.
试题解析:(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
∴AC=AB=9,AE=AD=6...
(1)138°;(2)3.
【解析】试题分析:(1)根据全等求出∠EBA的度数,根据邻补角的定义求出即可;
(2)根据全等三角形的性质得出AC=AB=9,AE=AD=6,即可求出答案.
试题解析:(1)∵△ABE≌△ACD,
∴∠EBA=∠C=42°,
∴∠EBG=180°-42°=138°;
(2)∵△ABE≌△ACD,
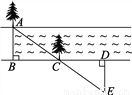
∴AC=AB=9,AE=AD=6... 某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20步有一棵树C,继续前行20步到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长就是河宽AB.
请你说明他们做法的正确性.
 见解析
【解析】分析:将题目中的实际问题转化为数学问题,然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性.
本题解析:
∵在△ABC和△EDC中,∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,
∴Rt△ABC≌Rt△EDC,
∴AB=ED,
即他们的做法是正确的.
见解析
【解析】分析:将题目中的实际问题转化为数学问题,然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性.
本题解析:
∵在△ABC和△EDC中,∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,
∴Rt△ABC≌Rt△EDC,
∴AB=ED,
即他们的做法是正确的. 如图是一副三角尺叠放的示意图,则∠α=______.
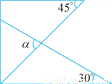
 75°
【解析】如图,由已知可得∠1=45°,∴由三角形外角的性质可得:∠2=45°+30°=75°,
又∵∠=∠2,
∴∠=75°.
75°
【解析】如图,由已知可得∠1=45°,∴由三角形外角的性质可得:∠2=45°+30°=75°,
又∵∠=∠2,
∴∠=75°. 杨辉三角是一个由数字排列成昀三角形数表,一般形式如图所示,其中每一横行都表示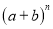 (此处
(此处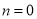 ,
, 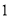 ,
, 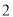 ,
, 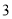 ,
, 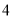 ,
, 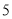 ,
, 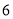 )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字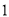 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.
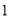
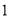
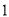
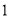
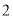
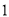
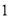
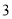
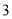
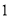
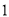
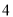
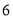
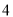
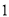
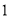
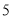
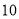
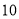
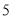
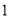
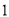
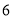
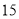
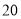
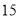
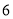
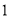
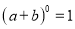
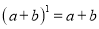
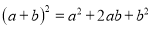
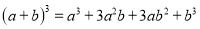
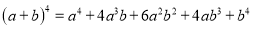
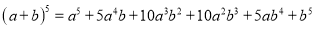
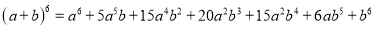
上图的构成规律你看懂了吗?
请你直接写出(a+b)7 =______.
杨辉三角还有另一个特征
(1)从第二行到第五行,每一行数字组成的数(如第三行为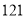 )都是上一行的数与______积.
)都是上一行的数与______积.
(2)由此你可写出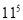 =______.
=______.
(3)由第_____行可写出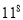 =______.
=______.
 (1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1...
(1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1... 当x=-2时,代数式ax3+bx+1的值是2 017,那么当x=2时,代数式ax3+bx+1的值是____.
 -2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015.
-2015
【解析】∵当x=-2时,代数式ax3+bx+1的值是2 017,
∴-8a-2b+1=2017,
即8a+2b=-2016.
∴当x=2时, ax3+bx+1=8a+2b+1=-2016+1=-2015. 在如图边长为7.6的正方形的角上挖掉一个边长为2.6的小正方形,剩余的图形能否拼成一个矩形?若能,画出这个矩形,并求出这个矩形的面积是多少.

 能,这个矩形的面积=(7.6+2.6)(7.6-2.6)=51
【解析】此题主要考查了乘法的平方差公式.即两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式
能,这个矩形的面积=(7.6+2.6)(7.6-2.6)=51
【解析】此题主要考查了乘法的平方差公式.即两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式 若x、y表示有理数,则下列各数中一定是正数的是( )
A. 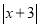 B.
B. 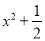 C.
C. 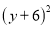 D.
D. 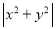
 B
【解析】试题分析:A、|x+3|≥0,故此选项错误;
B、x2≥0,x2+≥>0,故此选项正确;
C、(y+6)2≥0,故此选项错误;
D、|x2+y2|≥0,故此选项错误.
故选B.
B
【解析】试题分析:A、|x+3|≥0,故此选项错误;
B、x2≥0,x2+≥>0,故此选项正确;
C、(y+6)2≥0,故此选项错误;
D、|x2+y2|≥0,故此选项错误.
故选B. 
