题目内容
某段河流的两岸是平行的，数学兴趣小组在老师带领下不用涉水过河就测得河的宽度，他们是这样做的：
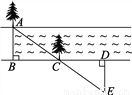
①在河流的一条岸边B点，选对岸正对的一棵树A；
②沿河岸直走20步有一棵树C，继续前行20步到达D处；
③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；
④测得DE的长就是河宽AB.
请你说明他们做法的正确性．
见解析
【解析】分析：将题目中的实际问题转化为数学问题，然后利用全等三角形的判定方法证得两个三角形全等即可说明其做法的正确性．
本题解析：
∵在△ABC和△EDC中，∠ABC=∠EDC=90°，BC=DC，∠ACB=∠ECD，
∴Rt△ABC≌Rt△EDC，
∴AB=ED，
即他们的做法是正确的.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图,∠1的内错角是( )
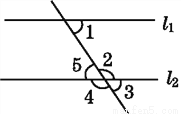
A. ∠2 B. ∠3 C. ∠4 D. ∠5
D
【解析】试题分析：根据内错角位于截线异侧，位于两条被截线之间可知∠1的内错角是∠5．
故选D． 如图，已知AE=DB，BC=EF，AC=DF，求证：（1）AC∥DF；（2）CB∥EF．
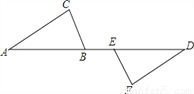
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由SSS证明△ABC≌△DEF，得出对应角相等∠A=∠D，∠ABC=∠DEF，由内错角相等即可得出结论；
（2）由（1）得：∠ABC=∠DEF，得出∠CBE=∠FEB，由内错角相等即可得出结论．
试题解析：（1）∵AE=DB，
∴AE-BE=DB-BE，
即AB=DE，
在△ABC和△DEF中，
，... 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（ ）
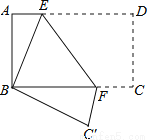
A. 3 B. 4 C. 6 D. 8
C
【解析】试题分析：由折叠特性可得CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，推出∠ABE=∠C′BF，所以△BAE≌△BC′F，根据△ABE和△BC′F的周长=2△ABE的周长求解．
【解析】
将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，
由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC... 下列说法正确的有( )
①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;
③面积相等的两个图形全等;
④周长相等的两个图形全等.
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①两个图形全等，它们的形状相同，故正确；
②两个图形全等，它们的大小相同，故正确；
③面积相等的两个图形全等，错误；
④周长相等的两个图形全等，错误.
故选：B. 一角为80°的三角形中，另两角的角平分线相交所成的锐角是________．
50°
【解析】∵∠A=80°，
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°，
∵OB、OC分别是∠ABC、∠ACB的平分线，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=×100°=50°，
在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°-50°=130°，
∴∠CO... 如图，为测量B点到河对面的目标A之间的距离，他们在B点同侧选择了一点C，测得∠ABC＝70°，∠ACB＝40°，然后在M处立了标杆，使∠CBM＝70°，∠BCM＝40°，那么需要测量________才能测得A，B之间的距离( )
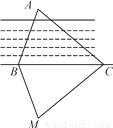
A. AB B. AC C. BM D. CM
C
【解析】∵∠ABC=∠CBM=70°，BC=BC，∠ACB=∠MCB=40°，
∴△ABC≌△MBC，∴AB=BM，
所以需要测量BM的长才能测得A、B之间的距离，
故选C. 在代数式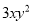
， 
， 
， 
， 
， 
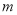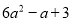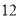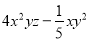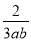中，单项式有___个，多项式有____个。
3 2
【解析】单项式有：3xy2，m，12，共3个，多项式有：6a2-a+3，4x2yz-xy2，共2个.
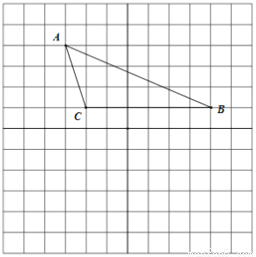
故答案为：3，2. 如图，将三角形ABC放在12*12的正方形网格中，每个小正方形的边长均为1，点A，B，C在格点上
（1）三角形ABC的面积是
（2）画出以点C为旋转中心，将三角形ABC按顺时针方向旋转90度后的三角形A’B’C’
（1）9；（2）见解析.
【解析】试题分析：（1）由图可知BC＝6，BC边上的高为3，根据三角形的面积公式即可得出结果；
（2）根据旋转的性质，分别画出A点和B点的对应点A’、B’，然后连接A’C，A’B’，B’C即可．
试题解析：
（1）由图可知BC＝6，BC边上的高为3，
所以三角形ABC的面积是×6×3＝9；
（2）如图：