题目内容
杨辉三角是一个由数字排列成昀三角形数表,一般形式如图所示,其中每一横行都表示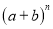 (此处
(此处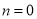 ,
, 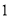 ,
, 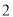 ,
, 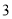 ,
, 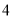 ,
, 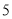 ,
, 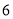 )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字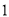 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.
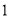
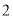
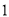
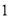
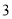
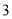
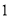
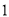
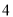
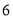
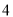
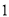
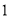
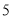
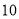
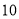
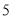
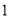
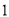
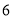
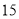
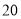
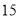
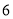
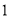
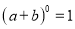
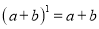
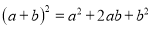
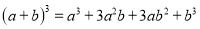
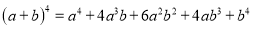
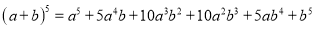
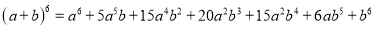
上图的构成规律你看懂了吗?
请你直接写出(a+b)7 =______.
杨辉三角还有另一个特征
(1)从第二行到第五行,每一行数字组成的数(如第三行为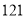 )都是上一行的数与______积.
)都是上一行的数与______积.
(2)由此你可写出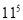 =______.
=______.
(3)由第_____行可写出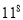 =______.
=______.
 (1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1...
(1)11 (2)161051 (3)9;214358881
【解析】试题分析:观察图表寻找规律:三角形是一个有数字排列形成的三角形数表,它的两条斜边都是数字1组成,而其余的数则是等于它“肩”上的两个数之和.
试题解析:
(1)从第二行到第五行,每一行数字组成的数(如第三行为)都是上一行的数与11的积.
(2)115=(10+1)5=105+5×104×1+10×103×1...
如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
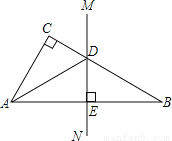
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
 (1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C...
(1)∠B=35°;(2)∠CAD=10°;(3)∠CAB=54°.
【解析】试题分析:(1)根据直角三角形的性质求出∠ADC=70°,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(2)根据直角三角形的性质求出∠B的度数,根据线段的垂直平分线的性质得到DA=DB,计算即可;
(3)设∠CAD=x,根据题意列出方程,解方程即可.
试题解析:(1)∵∠C=90°,∠C... 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
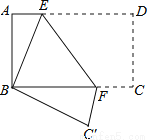
A. 3 B. 4 C. 6 D. 8
 C
【解析】试题分析:由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
【解析】
将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC...
C
【解析】试题分析:由折叠特性可得CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,推出∠ABE=∠C′BF,所以△BAE≌△BC′F,根据△ABE和△BC′F的周长=2△ABE的周长求解.
【解析】
将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,
由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC... 一角为80°的三角形中,另两角的角平分线相交所成的锐角是________.
 50°
【解析】∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵OB、OC分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°,
∴∠CO...
50°
【解析】∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵OB、OC分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-50°=130°,
∴∠CO... 如图,为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,∠BCM=40°,那么需要测量________才能测得A,B之间的距离( )
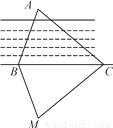
A. AB B. AC C. BM D. CM
 C
【解析】∵∠ABC=∠CBM=70°,BC=BC,∠ACB=∠MCB=40°,
∴△ABC≌△MBC,∴AB=BM,
所以需要测量BM的长才能测得A、B之间的距离,
故选C.
C
【解析】∵∠ABC=∠CBM=70°,BC=BC,∠ACB=∠MCB=40°,
∴△ABC≌△MBC,∴AB=BM,
所以需要测量BM的长才能测得A、B之间的距离,
故选C. (1) 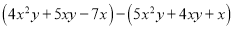 (2)
(2) 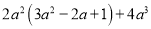
(3) 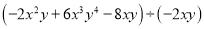 (4)2x3·(-x)2-(-x2)2·(-3x);.
(4)2x3·(-x)2-(-x2)2·(-3x);.
(5) (2x-y)2·(2x+y)2
 (1) (2) (3) (4) 5x5 (5) 16x4-8x2y2+y4
【解析】试题分析:(1)根据去括号法则和合并同类项法则求解即可;
(2)根据单项式乘以多项式法则计算,然后化简即可;
(3)根据除以单项式即可求解;
(4)根据幂的运算性质计算即可;
(5)根据平方差公式和完全平方公式计算即可.
试题解析:(1)
=4x2y+5xy-7x-5x2y...
(1) (2) (3) (4) 5x5 (5) 16x4-8x2y2+y4
【解析】试题分析:(1)根据去括号法则和合并同类项法则求解即可;
(2)根据单项式乘以多项式法则计算,然后化简即可;
(3)根据除以单项式即可求解;
(4)根据幂的运算性质计算即可;
(5)根据平方差公式和完全平方公式计算即可.
试题解析:(1)
=4x2y+5xy-7x-5x2y... 在代数式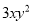 ,
, 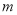 ,
, 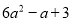 ,
, 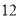 ,
, 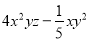 ,
, 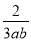 中,单项式有___个,多项式有____个。
中,单项式有___个,多项式有____个。
 3 2
【解析】单项式有:3xy2,m,12,共3个,多项式有:6a2-a+3,4x2yz-xy2,共2个.
故答案为:3,2.
3 2
【解析】单项式有:3xy2,m,12,共3个,多项式有:6a2-a+3,4x2yz-xy2,共2个.
故答案为:3,2. 2x3·(-x)2-(-x2)2·(-3x).
 5x5
【解析】试题分析:先算乘方,再算乘除,最后算加减即可.
试题解析:
2x3·(-x)2-(-x2)2·(-3x);.
=
=
=5x5
5x5
【解析】试题分析:先算乘方,再算乘除,最后算加减即可.
试题解析:
2x3·(-x)2-(-x2)2·(-3x);.
=
=
=5x5 下列各组中的两项,不是同类项的是( )
A. -2与π B. 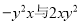 C.
C. 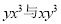 D.
D. 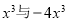
 C
【解析】试题分析:A、常数项与常数项是同类项,符合同类项的定义,故本选项不符合题意;
B、符合同类项的定义,故本选项不符合题意;
C、相同之母的指数不同,不是同类项,故本选项符合题意;
D、符合同类项的定义,故本选项不符合题意.
故选C.
C
【解析】试题分析:A、常数项与常数项是同类项,符合同类项的定义,故本选项不符合题意;
B、符合同类项的定义,故本选项不符合题意;
C、相同之母的指数不同,不是同类项,故本选项符合题意;
D、符合同类项的定义,故本选项不符合题意.
故选C. 
