题目内容
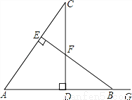
如图，CD⊥AB于点D，BE⊥AC于点E，△ABE≌△ACD，∠C=42°，AB=9，AD=6，G为AB延长线上一点．
（1）求∠EBG的度数．
（2）求CE的长．
(1)138°；（2）3.
【解析】试题分析：（1）根据全等求出∠EBA的度数，根据邻补角的定义求出即可；
（2）根据全等三角形的性质得出AC=AB=9，AE=AD=6，即可求出答案．
试题解析：（1）∵△ABE≌△ACD，
∴∠EBA=∠C=42°，
∴∠EBG=180°-42°=138°；
（2）∵△ABE≌△ACD，
∴AC=AB=9，AE=AD=6...
练习册系列答案
相关题目
下列各数中，负数是 （ ）
A. －(－5) B. －｜－5｜ C. (－5)2 D. －(－5)3．
B
【解析】A. －(－5)=5，是正数；
B. －｜－5｜=-5，是负数；
C. (－5)2 =25，是正数；
D. －(－5)3=-（-125）=125，是正数.
故选B. 如图，△ABC中，∠BAC=100°，DF，EG分别是AB，AC的垂直平分线，则∠DAE等于（ ）
A. 50° B. 45° C. 30° D. 20°
D
【解析】试题解析：根据线段的垂直平分线性质，可得AD=BD，AE=CE．
故∠EAC=∠ECA，∠ABD=∠BAD．
因为∠BAC=100°，∠ABD+∠ACE=180°-100°=80°，
∴∠DAE=100°-∠BAD-∠EAC=20°．
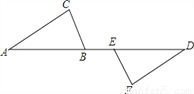
故选D. 如图，已知AE=DB，BC=EF，AC=DF，求证：（1）AC∥DF；（2）CB∥EF．
（1）证明见解析（2）证明见解析
【解析】试题分析：（1）由SSS证明△ABC≌△DEF，得出对应角相等∠A=∠D，∠ABC=∠DEF，由内错角相等即可得出结论；
（2）由（1）得：∠ABC=∠DEF，得出∠CBE=∠FEB，由内错角相等即可得出结论．
试题解析：（1）∵AE=DB，
∴AE-BE=DB-BE，
即AB=DE，
在△ABC和△DEF中，
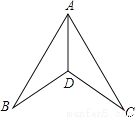
，... 如图，AB=AC，BD=CD，则△ABD≌△ACD的依据是（ ）
A. SSS B. SAS C. AAS D. HL
A
【解析】在△ABD和△ACD中，
，
∴△ABD和△ACD（SSS）；
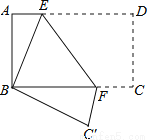
故选：A. 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，若AB=1，BC=2，则△ABE和△BC′F的周长之和为（ ）
A. 3 B. 4 C. 6 D. 8
C
【解析】试题分析：由折叠特性可得CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC′=∠ABC=90°，推出∠ABE=∠C′BF，所以△BAE≌△BC′F，根据△ABE和△BC′F的周长=2△ABE的周长求解．
【解析】
将矩形纸片ABCD折叠，使点D与点B重合，点C落在C′处，折痕为EF，
由折叠特性可得，CD=BC′=AB，∠FC′B=∠EAB=90°，∠EBC... 下列说法正确的有( )
①两个图形全等,它们的形状相同;
②两个图形全等,它们的大小相同;
③面积相等的两个图形全等;
④周长相等的两个图形全等.
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】①两个图形全等，它们的形状相同，故正确；
②两个图形全等，它们的大小相同，故正确；
③面积相等的两个图形全等，错误；
④周长相等的两个图形全等，错误.
故选：B. 如图，为测量B点到河对面的目标A之间的距离，他们在B点同侧选择了一点C，测得∠ABC＝70°，∠ACB＝40°，然后在M处立了标杆，使∠CBM＝70°，∠BCM＝40°，那么需要测量________才能测得A，B之间的距离( )
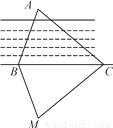
A. AB B. AC C. BM D. CM
C
【解析】∵∠ABC=∠CBM=70°，BC=BC，∠ACB=∠MCB=40°，
∴△ABC≌△MBC，∴AB=BM，
所以需要测量BM的长才能测得A、B之间的距离，
故选C. 若(2x＋1)0＝1，则x的取值范围是_____.
x≠-
【解析】任何一个不等于零的数的零次幂都等于1.由此可得2x+1≠0，解得，所以当(2x＋1)0＝1，x的取值范围是.