题目内容
18．
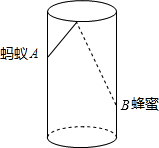如图，圆柱形容器杯高16cm，底面周长20cm，在离杯底3cm的点B处有一滴蜂蜜，此时蚂蚁在离杯上沿2cm与蜂蜜相对的A处，则蚂蚁从A处爬到B处的蜂蜜最短距离为5$\sqrt{13}$．
分析 将杯子侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′B的长度即为所求．
解答 
解：如图，将杯子侧面展开，作A关于EF的对称点A′，
连接A′B，则A′B即为最短距离，
在直角△A′DB中，由勾股定理得
A′B=$\sqrt{A′{D}^{2}+D{B}^{2}}$=5$\sqrt{13}$$\sqrt{221}$（cm）．
故答案为：5$\sqrt{13}$．
点评 本题考查了平面展开---最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
有一小球在如图所示的地板上自由滚动，地板上的每个三角形均为等边三角形，则小球在地板上最终停留在黑色区域的概率为$\frac{1}{4}$．
如图，AD是△ABC的中线．求证：AE•FC=2AF•DE．
如图，△ABO和△CDO是以点O为位似中心的位似图形，若点A（3，4），点C（1.5，2），点D（2，1），则点D的对应点B的坐标是（4，2）．