题目内容
13.设a为有理数,x为无理数,证明:(1)a+x是无理数;(2)当a≠0时,ax是无理数.分析 利用反证法,结合任何有理数都可以表示成$\frac{q}{p}$的形式(p,q都是整数),反过来也一样,任何形如$\frac{q}{p}$(p,q都是整数)的数都是有理数,即可证明结论.
解答 证明:(1)任何有理数都可以表示成$\frac{q}{p}$的形式(p,q都是整数),反过来也一样,任何形如$\frac{q}{p}$(p,q都是整数)的数都是有理数,
∵a为有理数,
∴a=$\frac{q}{p}$.
如果a+x是有理数,那么a+x=$\frac{q′}{p′}$,x=$\frac{q′}{p′}$-a=$\frac{q′}{p′}$-$\frac{q}{p}$=$\frac{pq′-qp′}{pp′}$,
那么x是有理数,这与x为无理数矛盾,
所以a+x为无理数;
(2)如果ax是有理数,那么ax=$\frac{q′}{p′}$,x=$\frac{pq′}{qp′}$
所以x是有理数,这与x为无理数矛盾,
所以当a≠0时,ax为无理数.
点评 本题考查了反证法,考查学生分析解决问题的能力,正确运用反证法是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
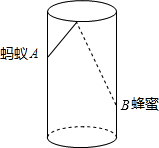 如图,圆柱形容器杯高16cm,底面周长20cm,在离杯底3cm的点B处有一滴蜂蜜,此时蚂蚁在离杯上沿2cm与蜂蜜相对的A处,则蚂蚁从A处爬到B处的蜂蜜最短距离为5$\sqrt{13}$.
如图,圆柱形容器杯高16cm,底面周长20cm,在离杯底3cm的点B处有一滴蜂蜜,此时蚂蚁在离杯上沿2cm与蜂蜜相对的A处,则蚂蚁从A处爬到B处的蜂蜜最短距离为5$\sqrt{13}$. 如图,a,b,c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为70°.
如图,a,b,c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为70°.
 已知:如图,正方形ABCD,∠ECF=135°,∠BCE=∠DCG=∠GCH.求证:H为EF的中点.
已知:如图,正方形ABCD,∠ECF=135°,∠BCE=∠DCG=∠GCH.求证:H为EF的中点. 如图,在?ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于25°.
如图,在?ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于25°.