题目内容
7. 某校墙边有甲、乙两根木杆.
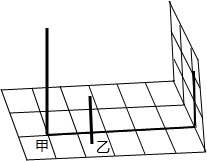
某校墙边有甲、乙两根木杆.(1)某一时刻甲木杆在阳光下的影子如图所示,你能画出此时乙木杆的影子吗?
(2)若1米高的木杆影长为0.8米,乙木杆落在墙上的影子为0.4米,那么乙木杆移动到什么位置时,其影子刚好不落在墙上?
分析 (1)利用甲木杆在阳光下的影子得到太阳光线,再利用平行投影得到乙木杆的影子;
(2)根据“在同一时刻物高与影长的比相等“得到$\frac{BC}{BE}$=$\frac{1}{0.8}$,解得BE=0.32,于是把乙木杆向左移动0.32米时,其影子刚好不落在墙上.
解答 解:(1)如图,乙木杆落在地上的影子为AB,落墙上的影子为BC;
(2)延长DC和AB交于点E,如图,
根据题意得$\frac{BC}{BE}$=$\frac{1}{0.8}$,即$\frac{0.4}{BE}$=$\frac{1}{0.8}$,解得BE=0.32,
所以乙木杆向左移动0.32米时,其影子刚好不落在墙上.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.也考查了平行投影.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.写出满足如表条件的一次函数表达式为y=-3x+1.
| x | -1 | 0 | 1 | 2 |
| y | 4 | 1 | -2 | -5 |
19.直线y=-3x+1上有一点P,且点P到y轴的距离是1,则点P的坐标为( )
| A. | (1,-2) | B. | (-1,4) | C. | (1,-2)或(-1,4) | D. | 以上都不对 |
17.已知x+$\frac{1}{x}$=5,则${x^2}+\frac{1}{x^2}$的值为( )
| A. | 9 | B. | 5 | C. | 23 | D. | 25 |
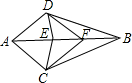 如图,已知AC=AD,BC=BD,CE=DE,则全等三角形共有6对.
如图,已知AC=AD,BC=BD,CE=DE,则全等三角形共有6对. 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
