题目内容
6. 如图,已知矩形ABCD中,E是边BC的中点,将△ABE沿直线AE折叠,点B落在点F处,连接AF并延长交边BC的延长线于点G,连接FC,若sin∠FCE=$\frac{4}{5}$,CG=3,求FC的长.
如图,已知矩形ABCD中,E是边BC的中点,将△ABE沿直线AE折叠,点B落在点F处,连接AF并延长交边BC的延长线于点G,连接FC,若sin∠FCE=$\frac{4}{5}$,CG=3,求FC的长.
分析 由E是边BC的中点,得到BE=CE,根据折叠的性质得到BE=EF,∠1=$\frac{1}{2}∠$BAF,得到BE=EF=CE,根据矩形的性质得到∠B=90°,根据余角的性质得到∠BAG=∠FEG=90°,过E作EH⊥CF于H,推出∠AEB=∠ECF,根据平行线的判定定理得到AE∥CF,设AB=4k,AE=5k,勾股定理得到BE=3k,根据相似三角形的性质即可得到结论.
解答 解:∵E是边BC的中点,
∴BE=CE,
∵将△ABE沿直线AE折叠得到△AFE,
∴BE=EF,∠1=$\frac{1}{2}∠$BAF,
∴BE=EF=CE,
∵四边形ABCD是矩形,
∴∠B=90°,
∴∠AFE=∠EFG=90°,
∴∠BAG+∠G=∠FEG+∠G=90°,
∴∠BAG=∠FEG=90°,
过E作EH⊥CF于H,
∴∠2=$\frac{1}{2}$∠CEF,
∴∠1=∠2,
∴∠AEB=∠ECF,
∴AE∥CF,
∵sin∠FCE=$\frac{4}{5}$,
∴sin∠AEB=$\frac{AB}{AE}$=$\frac{4}{5}$,
∴设AB=4k,AE=5k,
∴BE=3k,
∴EF=CE=3k,
∵∠B=∠CHE=90°,∠1=∠2,
∴△ABE∽△EHC,
∴∴$\frac{AE}{CE}=\frac{BE}{CH}$,
∴CH=$\frac{9}{5}$k,
∴CF=2CH=$\frac{18}{5}$k,
∵AE∥CF,
∴△CFG∽△EAG,
∴$\frac{CF}{AE}$=$\frac{CG}{EG}$,
即$\frac{\frac{18}{5}k}{5k}$=$\frac{3}{3+3k}$,
∴k=$\frac{7}{18}$,
∴CF=$\frac{7}{5}$.
点评 本题考查了翻折变换(折叠问题),相似三角形的判定和性质,矩形的性质,等腰三角形的判定和性质,正确作出辅助线是解题的关键.

| A. | 15 | B. | -15 | C. | 8 | D. | -8 |
| A. | (-0.5,0.5) | B. | (0.5,-0.5) | C. | (-0.5,-0.5) | D. | (0.5,0.5) |
 如图,在平行四边形ABCD中,AE=EB,AF=2,则FC的值为( )
如图,在平行四边形ABCD中,AE=EB,AF=2,则FC的值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
| A. | 两直线平行,同位角相等 | |
| B. | 两点之间线段最短 | |
| C. | 对顶角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
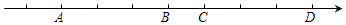 如图,数轴上相邻刻度间的线段表示一个单位长度,点A、B、C、D对应的数a、b、c、d,且2a+b+d=2,那么数轴的原点应是( )
如图,数轴上相邻刻度间的线段表示一个单位长度,点A、B、C、D对应的数a、b、c、d,且2a+b+d=2,那么数轴的原点应是( )