题目内容
5. 如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=6cm,AC=4cm,则AD的长为$\frac{12\sqrt{3}}{5}$cm.
如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=6cm,AC=4cm,则AD的长为$\frac{12\sqrt{3}}{5}$cm.
分析 作辅助线,构建平行线和垂线,先根据外角定理和角平分线性质得:∠BAD=∠N,由等角对等边得:BN=AB=6,由三角函数求AE的长,根据等腰三角形三线合一得AN的长,证明△BND∽△CAD,根据线段的长设未知数列等式可得结论.
解答 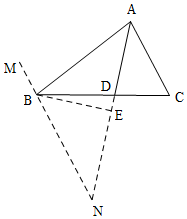 解:过B作BM∥AC,交AD的延长线于点N,作BE⊥AN于E,
解:过B作BM∥AC,交AD的延长线于点N,作BE⊥AN于E,
∵BM∥AC,
∴∠MBA=∠BAC=60°,
∵AD平分∠BAC,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴∠N=∠MBA-∠BAD=60°-30°=30°
∴∠BAD=∠N,
∴BN=AB=6,
在Rt△ABE中,
AE=AB•cos∠BAD=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴AN=2AE=6$\sqrt{3}$,
∵BM∥AC,
∴△BND∽△CAD,
∴$\frac{AD}{DN}=\frac{AC}{BN}$=$\frac{4}{6}=\frac{2}{3}$,
设AD=2x,则DN=3x,
而AD+DN=AN,
∴2x+3x=6$\sqrt{3}$,
x=$\frac{6\sqrt{3}}{5}$,
∴AD=$\frac{12\sqrt{3}}{5}$cm.
故答案为:$\frac{12\sqrt{3}}{5}$.
点评 本题考查了相似三角形的性质和判定,把求线段的长的问题转化为求三角形相似的问题解决,正确作出辅助线是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.若-1<m<0,m,m2,$\frac{1}{m}$的大小关系是( )
| A. | $\frac{1}{m}$<m<m2 | B. | m<m2<$\frac{1}{m}$ | C. | m2<m<$\frac{1}{m}$ | D. | $\frac{1}{m}$<m2<m |
 如图,四边形ABCD和AEFG分别是长方形和正方形,已知正方形的边长是10,△DFG的面积是18.求长方形ABCD的面积.
如图,四边形ABCD和AEFG分别是长方形和正方形,已知正方形的边长是10,△DFG的面积是18.求长方形ABCD的面积.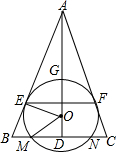 如图,O为等腰三角形ABC内一点,⊙O与底边BC交于M、N两点,且与AB、AC相切于E、F两点,连接AO,与⊙O交于点G,与BC相交于点D.
如图,O为等腰三角形ABC内一点,⊙O与底边BC交于M、N两点,且与AB、AC相切于E、F两点,连接AO,与⊙O交于点G,与BC相交于点D. 作图题
作图题