题目内容
10.一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下(单位:米):+7、-4、+3、-11、-6、+12、-10(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门线最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
分析 (1)由于守门员从球门线出发练习折返跑,问最后是否回到了球门线的位置,只需将所有数加起来,看其和是否为0即可;
(2)计算每一次跑后的数据,绝对值最大的即为所求;
(3)求出所有数的绝对值的和即可.
解答 解:(1)(+7)+(-4)+(+3)+(-11)+(-6)+(+12)+(-10)
=(7+3+12)-(4+11+6+10)
=22-31
=-9
答:守门员最后回到了球门线的位置.
(2)7-4=3,
3+3=6,
6-11=-5,
-5-6=-11,
-11+12=1,
1-10=-9,
答:在练习过程中,守门员离开球门线最远距离是11米.
(3)|+7|+|-4|+|+3|+|-11|+|-6|+|+12|+|-10|
=7+4+3+11+6+12+10
=53米.
答:守门员全部练习结束后,他共跑了53米.
点评 此题考查了正数和负数,在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.“正”和“负”相对.解题关键是理解“正”和“负”的相对性,确定具有相反意义的量.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
3.一个三角形的两个内角分别为60°和20°,则这个三角形是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 不能确定 |
20.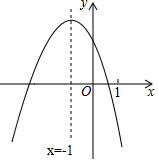 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠-1);③关于x的一元二次方程ax2+(b-1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:①4a+c<0;②m(am+b)+b>a(m≠-1);③关于x的一元二次方程ax2+(b-1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.有理数a,b在数轴上的位置如图所示,那么下列式子中成立的是( )


| A. | ab>0 | B. | $\frac{a}{b}>0$ | C. | a-1>0 | D. | a<b |
20.下列命题为真命题的是( )
| A. | 两直线平行,同位角相等 | B. | 若a⊥b,b⊥c,则a⊥c | ||
| C. | 邻补角是互补的角 | D. | 两个锐角的和是锐角 |
 如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=6cm,AC=4cm,则AD的长为$\frac{12\sqrt{3}}{5}$cm.
如图所示,在△ABC中,∠BAC=60°,∠BAC的平分线交BC于D.若AB=6cm,AC=4cm,则AD的长为$\frac{12\sqrt{3}}{5}$cm.